Article contents
SEMIREGULAR FACTORIZATIONS OF REGULAR MULTIGRAPHS
Published online by Cambridge University Press: 13 July 2010
Abstract
An (r,r+1)-factor of a graph G is a spanning subgraph H such that dH(v)∈{r,r+1} for all vertices v∈𝒱(G). If G is expressed as the union of edge-disjoint (r,r+1)-factors, then this expression is an (r,r+1)-factorization of G. Let μ(r) be the smallest integer with the property that if G is a regular loopless multigraph of degree d with d≥μ(r), then G has an (r,r+1)-factorization. It is shown that 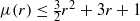 if r is even. The proof employs a novel list-coloring approach. Together with known results, this shows that μ(r)=r2+1 if r is odd and
if r is even. The proof employs a novel list-coloring approach. Together with known results, this shows that μ(r)=r2+1 if r is odd and 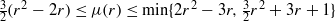 if r is even.
if r is even.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2010
References
- 1
- Cited by


