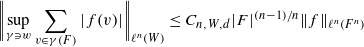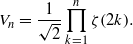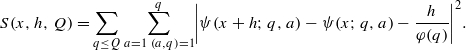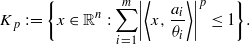Research Article
THE KAKEYA SET AND MAXIMAL CONJECTURES FOR ALGEBRAIC VARIETIES OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 1-25
-
- Article
- Export citation
ON SHRINKING TARGETS FOR ℤm ACTIONS ON TORI
- Part of:
-
- Published online by Cambridge University Press:
- 16 April 2010, pp. 193-202
-
- Article
- Export citation
AN EXTENSION OF A THEOREM OF HLAWKA
-
- Published online by Cambridge University Press:
- 29 April 2010, pp. 203-216
-
- Article
- Export citation
INFINITE PATHS WITH NO SMALL ANGLES
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 26-34
-
- Article
- Export citation
TILINGS OF HILBERT SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 29 April 2010, pp. 217-230
-
- Article
- Export citation
A NOTE ON THE SECOND MOMENT OF AUTOMORPHIC L-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 35-44
-
- Article
- Export citation
ON THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2010, pp. 231-243
-
- Article
- Export citation
VOLUME ESTIMATES FOR Lp-ZONOTOPES AND BEST BEST CONSTANTS IN BRASCAMP–LIEB INEQUALITIES
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 45-60
-
- Article
- Export citation
ON THE MAXIMIZATION OF A CLASS OF FUNCTIONALS ON CONVEX REGIONS, AND THE CHARACTERIZATION OF THE FARTHEST CONVEX SET
- Part of:
-
- Published online by Cambridge University Press:
- 18 May 2010, pp. 245-265
-
- Article
- Export citation
RANDOM SUBSETS OF SELF-AFFINE FRACTALS
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 61-76
-
- Article
- Export citation
SIMULTANEOUS DIOPHANTINE APPROXIMATION ON POLYNOMIAL CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 77-85
-
- Article
- Export citation
COVARIOGRAM OF NON-CONVEX SETS
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2010, pp. 267-284
-
- Article
- Export citation
NEW RESULTS FOR T(k)-FAMILIES IN THE PLANE
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 86-92
-
- Article
- Export citation
ON STRICTLY SINGULAR OPERATORS BETWEEN SEPARABLE BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2010, pp. 285-304
-
- Article
- Export citation
SUPERCRITICAL TWO-FLUID INTERACTIONS WITH SURFACE TENSION AND GRAVITY
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 93-106
-
- Article
- Export citation
DAVENPORT’S METHOD AND SLIM EXCEPTIONAL SETS: THE ASYMPTOTIC FORMULAE IN WARING’S PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2010, pp. 305-321
-
- Article
- Export citation
NEW REPRESENTATIONS FOR APÉRY-LIKE SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 107-117
-
- Article
- Export citation
CORRESPONDENCE OF THE EIGENVALUES OF A NON-SELF-ADJOINT OPERATOR TO THOSE OF A SELF-ADJOINT OPERATOR
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2010, pp. 323-338
-
- Article
- Export citation
DISTRIBUTION OF INTEGER LATTICE POINTS IN A BALL CENTRED AT A DIOPHANTINE POINT
- Part of:
-
- Published online by Cambridge University Press:
- 10 December 2009, pp. 118-134
-
- Article
- Export citation
STABILITY OF THE PRÉKOPA–LEINDLER INEQUALITY
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2010, pp. 339-356
-
- Article
- Export citation