On capitulation in certain Z_l-extensions of number fields

Extract

Let F be a number field, l a prime, and K a normal extension of F for which Gal(K/F) is topologically isomorphic to the additive group Z_l. Then, corresponding to the subgroups lⁿ Z_l, there is a chain of fields F = F₀ ⊂ F₁ ⊂ F₂ ⊂ … ⊂ K so that Gal (F_n/F) is cyclic of order lⁿ. Let A_n be the l-Sylow subgroup of the ideal class group of F_n. By the now well-known theorem of Iwasawa, there are constants μ, λ and ν so that, for all sufficiently large n, |A_n| = l^e_n, where e_n = μlⁿ + λn + ν. Much work has been done investigating these constants, especially showing μ to be 0 for cyclotomic Z_l-extensions of abelian fields F, [2], and computing λ and ν in special cases. In many cases, it has been shown that μ = λ = 0, and I know of no cases where μ or λ are positive when F is totally real (cf. Greenberg [3]). Here we investigate the maps i_n,m: A_n → A_m induced by the inclusion of F_n in F_m for m ≥ n, with a view to determining their kernels. When μ = λ = 0, we prove that i_{n, n+s}(A_n) = 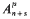for large enough n, and that, for large enough n, Ker i_{n, n+s} coincides with the kernel of the l^s power map on A_n. I thank A. Brumer for helpful conversations on this matter.