Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beck, J.
and
Chen, W. W. L.
1993.
Irregularities of point distribution relative to convex polygons II.
Mathematika,
Vol. 40,
Issue. 1,
p.
127.
Matousěk, Jiří
1997.
On discrepancy bounds
via
dual shatter function
.
Mathematika,
Vol. 44,
Issue. 1,
p.
42.
Yomdin, Yosef
2009.
Characteristic Functions, Scattering Functions and Transfer Functions.
p.
375.
Chen, William
and
Vaughan, Robert
2017.
Klaus Friedrich Roth. 29 October 1925 — 10 November 2015.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 63,
Issue. ,
p.
487.
Chen, William
and
Vaughan, Robert
2018.
Klaus Friedrich Roth, 1925-2015.
Bulletin of the London Mathematical Society,
Vol. 50,
Issue. 3,
p.
529.


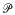 is a distribution of
is a distribution of