Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T05:07:39.415Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hausdorff measure of the intersection of sets of positive Lebesgue measure

Published online by Cambridge University Press:  26 February 2010

P. Erdös  and
S. J. Taylor
P. Erdös
Affiliation:
University College, London.
S. J. Taylor
Affiliation:
Westfield College, London.
Get access

Extract

Erdös, Kestelman and Rogers [1[ showed that, if A1, A2,… is any sequence of Lebesgue measurable subsets of the unit interval [0, 1] each of Lebesgue measure at least η > 0, then there is a subsequence {Ani} (i = 1, 2,…) such that the intersection 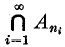contains a perfect subset (and is therefore of power 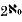). They asked for what Hausdorff measure functions φ(t) is it possible to choose the subsequence to make the intersection set ∩Ani of positive φ-measure. In the present note we show that the strongest possible result in this direction is true. This is given by the following theorem.

Type
Research Article
Information
Mathematika , Volume 10 , Issue 1 , June 1963 , pp. 1 - 9
Copyright
Copyright © University College London 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Erdös, P., Kestelman, H., and Rogers, C. A., “An intersection property of sets of positive measure”, to appear in Colloquium Math.Google Scholar
Erdös, P., Rogers, C. A., and Taylor, S. J., “Scales of functions”, Australian J. of Math., 1 (1960), 396–418.CrossRefGoogle Scholar
Rogers, C. A. and Taylor, S. J., “Functions continuous and singular with respect to a Hausdorff moasure”, Mathematika, 8 (1961), 1“31.CrossRefGoogle Scholar
Besicovitch, A. S., “On existence of subsets of finite measure of sets of infinite measure”, Indag. Math., 14 (1952), 339–344.CrossRefGoogle Scholar
Taylor, S. J., “On strengthening the Lebesgue density theorem”, Fund. Math., 46 (1959), 305–315.CrossRefGoogle Scholar