Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-17T18:47:48.840Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPLICIT ZERO-FREE REGIONS FOR DIRICHLET 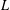$L$-FUNCTIONS

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  03 April 2018

Habiba Kadiri
Habiba Kadiri*
Affiliation:
Department of Mathematics and Computer Science, University of Lethbridge, 4401 University Drive, Lethbridge, Alberta T1K 3M4, Canada email [email protected]
Get access

Abstract

Let 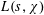$L(s,\unicode[STIX]{x1D712})$ be the Dirichlet 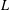$L$-function associated to a non-principal primitive character 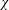$\unicode[STIX]{x1D712}$ modulo 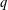$q$ with 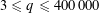$3\leqslant q\leqslant 400\,000$. We prove a new explicit zero-free region for 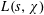$L(s,\unicode[STIX]{x1D712})$: 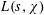$L(s,\unicode[STIX]{x1D712})$ does not vanish in the region 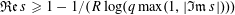$\mathfrak{Re}\,s\geqslant 1-1/(R\log (q\max (1,|\mathfrak{Im}\,s|)))$ with 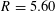$R=5.60$. This improves a result of McCurley where 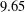$9.65$ was shown to be an admissible value fo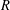r $R$.

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Mathematika , Volume 64 , Issue 2 , 2018 , pp. 445 - 474
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J.-H. and Kwon, S.-H., Some explicit zero-free regions for Hecke L-functions. J. Number Theory 145 2014, 433–473.CrossRefGoogle Scholar
Bennett, M., Rational approximation to algebraic numbers of small heights: the Diophantine equation ax n - by n = 1. J. Reine Angew. Math. 535 2001, 1–49.CrossRefGoogle Scholar
Bennett, M., Martin, G., O’Bryant, K. and Rechnitzer, A., Explicit bounds for primes in arithmetic progressions (in preparation).Google Scholar
Büthe, J., Estimating $\unicode[STIX]{x1D70B}(x)$ and related functions under partial RH assumptions. Preprint, 2015,arXiv:1410.7015.Google Scholar
Davenport, H., Multiplicative Number Theory, 3rd edn. (Graduate Texts in Mathematics 74 ), Springer (New York, 2000).Google Scholar
Dusart, P., Estimates of 𝜓, 𝜃 for large values of x without the Riemann hypothesis. Math. Comp. 85(298) 2016, 875–888.CrossRefGoogle Scholar
Faber, L. and Kadiri, H., New bounds for 𝜓(x). Math. Comp. 84(293) 2015, 1339–1357.CrossRefGoogle Scholar
Hajdu, L., Saradha, N. and Tijdeman, R., On a conjecture of Pomerance. Acta Arith. 155(2) 2012, 175–184.CrossRefGoogle Scholar
Heath-Brown, D. R., Zero-free regions for Dirichlet L-functions and the least prime in an arithmetic progression. Proc. Lond. Math. Soc. (3) 64(2) 1992, 265–338.CrossRefGoogle Scholar
Helfgott, H., Minor arcs for Goldbach’s problem. Preprint, 2012, arXiv:1205.5252v1.Google Scholar
Helfgott, H., Major arcs for Goldbach’s problem. Preprint, 2013, arXiv:1305.2897.Google Scholar
Jang, W. J. and Kwon, S. H., A note on Kadiri’s explicit zero-free region for Riemann zeta function. J. Korean Math. Soc. 51 2014, 1291–1304.CrossRefGoogle Scholar
Kadiri, H., Une région explicite sans zéro pour les fonctions $L$ de Dirichlet. PhD Thesis, Université Lille I, 2002.Google Scholar
Kadiri, H., Une région explicite sans zéros pour la fonction Zeta de Riemann. Acta Arith. 117(4) 2005, 303–339.CrossRefGoogle Scholar
Kadiri, H., Explicit zero-free regions for Dedekind zeta functions. Int. J. Number Theory 8(1) 2012, 1–23.CrossRefGoogle Scholar
Kadiri, H. and Lumley, A., Primes in arithmetic progressions. Preprint.Google Scholar
Kadiri, H. and Lumley, A., Short intervals containing primes. Integers A61 2014, 1–18.Google Scholar
Kondrateev, V. P., On some extremal properties of positive trigonometric polynomials. Mat. Zametki 22(3) 1977, 371–374.Google Scholar
McCurley, K. S., Explicit zero-free regions for Dirichlet L-functions. J. Number Theory 19 1984, 7–32.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I. Classical Theory, Cambridge University Press (2007).Google Scholar
Mossinghoff, M. and Trudgian, T., Nonnegative trigonometric polynomials and a zero-free region for the Riemann zeta-function. J. Number Theory 157(245) 2015, 329–349.CrossRefGoogle Scholar
Platt, D., Numerical computations concerning the GRH. Math. Comp. 85 2015, 3009–3027.CrossRefGoogle Scholar
Ramaré, O., Explicit estimates for the summatory function of 𝜆(n)/n from the one of 𝜆(n). Acta Arith. 159 2013, 113–122.CrossRefGoogle Scholar
Ramaré, O. and Rumely, R., Primes in arithmetic progressions. Math. Comp. 65(213) 1996, 397–425.CrossRefGoogle Scholar
Révész, S., On some extremal problems of Landau. Serdica Math. J. 33 2007, 125–132.Google Scholar
Rosser, J. B. and Schoenfeld, L., Sharper bounds for the Chebyshev functions 𝜃(x) and 𝜓(x). Math. Comp. 29(129) 1975, 243–269.Google Scholar
Stechkin, S. B., The zeros of the Riemann zeta-function. Math. Notes 8 1970, 706–711.CrossRefGoogle Scholar
Trudgian, T., An improved upper bound for the argument of the Riemann zeta-function on the critical line. Math. Comp. 81(278) 2012, 1053–1061.CrossRefGoogle Scholar
Trudgian, T., Updating the error term in the prime number theorem. Ramanujan J. 39(2) 2016, 225–234.CrossRefGoogle Scholar
Xylouris, T., On the least prime in an arithmetic progression and estimates for the zeros of Dirichlet L-functions. Acta Arith. 150 2011, 65–91.CrossRefGoogle Scholar