Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T05:56:27.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Central sets in commutative semigroups and partition regularity of systems of linear equations

Part of: Extremal combinatorics

Published online by Cambridge University Press:  26 February 2010

Neil Hindman  and
Wen-Jin Woan
Neil Hindman
Affiliation:
Department of Mathematics, Howard University, Washington, D.C. 20059, U.S.A.
Wen-Jin Woan
Affiliation:
Department of Mathematics, Howard University, Washington, D.C. 20059, U.S.A.
Get access

Abstract

Given a commutative semigroup (S, +) with identity 0 and u × v matrices A and B with nonnegative integers as entries, we show that if C = A – B satisfies Rado's columns condition over ℤ, then any central set in S contains solutions to the system of equations 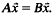. In particular, the system of equations 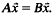is then partition regular. Restricting our attention to the multiplicative semigroup of positive integers (so that coefficients become exponents) we show that the columns condition over ℤ is also necessary for the existence of solutions in any central set (while the distinct notion of the columns condition over Q is necessary and sufficient for partition regularity over ℕ\{1}).

MSC classification

Secondary: 05D10: Ramsey theory
Type
Research Article
Information
Mathematika , Volume 40 , Issue 2 , December 1993 , pp. 169 - 186
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bergelson, V., Deuber, W., Hindman, N. and Lefmann, H.. Rado's Theorem for Commutative Rings. J. Comb. Theory (Series A). To appear.Google Scholar
2.Bergelson, V. and Hindman, N.. Nonmetrizable topological dynamics and Ramsey Theory. Trans. Amer. Math. Soc., 320 (1990), 293–300.CrossRefGoogle Scholar
3.Bergelson, V. and Hindman, N.. Ramsey Theory in non-commutative semigroups. Trans. Amer. Math. Soc., 330 (1992), 433–446.CrossRefGoogle Scholar
4.Berglund, J., Junghenn, H. and Milnes, P.. Analysis on Semigroups (Wiley, New York, 1989).Google Scholar
5.Curtis, C. and Reiner, I.. Representation Theory of Finite Groups and Associative Algebras (Wiley, New York, 1962).Google Scholar
6.Deuber, W.. Partitionen und lineare Gleichunssysteme. Math. Zeit., 133 (1973), 109–123.CrossRefGoogle Scholar
7.Ellis, R.. Lectures on Topological Dynamics (Benjamin, New York, 1969).Google Scholar
8.Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (Princeton Univ. Press, Princeton, 1981).CrossRefGoogle Scholar
9.Glasner, S.. Divisible properties and the Stone-Čech compactification. Canadian J. Math., 32 (1980), 993–1007.CrossRefGoogle Scholar
10.Graham, R., Rothschild, B. and Spencer, J.. Ramsey Theory (Wiley, New York, 1990).Google Scholar
11.Hindman, N.. Sums equal to products in βN. Semigroup Forum, 21 (1980), 221–255.CrossRefGoogle Scholar
12.Hindman, N.. The ideal structure of the space of к-uniform ultrafilters on a discrete semigroup. Rocky Mountain J. Math., 16 (1986), 685–701.CrossRefGoogle Scholar
13.Hindman, N.. Ultrafilters and combinatorial number theory. In Number Theory Carbondale 1979, Nathanson, M. ed., Lecture Notes in Math., 751 (1979), 119–184.Google Scholar
14.Lefmann, H.. On partition regular systems of equations. J. Comb. Theory (Series A), 58 (1991), 35–53.CrossRefGoogle Scholar
15.Rado, R.. Studien zur Kombinatorik. Math. Zeit., 36 (1933), 242–280.CrossRefGoogle Scholar