Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T05:38:27.071Z Has data issue: false hasContentIssue false
  • English
  • Français

An extension theorem for convex functions and an application to Teicher's characterization of the normal distribution

Part of: Real functions

Published online by Cambridge University Press:  26 February 2010

Wolfgang Stadje
Wolfgang Stadje
Affiliation:
Fachbereich Mathematik, Universität Osnabrück, Albrechtstrasse 28, 45 Osnabrück, West Germany.
Get access

Extract

The main aim of this note is the proof of the following

Let −∞ ≤ a > b ≤ ∞ and let A ⊂ (a, b) be a measurable set such that λ((a, b)\A) = 0, where λ denotes Lebesgue measure on ℝ. Let f: A→ℝ be a measurable and midconvex function, i.e.

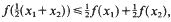
whenever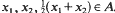. Then there exists a convex function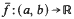such that.

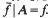MSC classification

Secondary: 26A51: Convexity, generalizations
Type
Research Article
Information
Mathematika , Volume 34 , Issue 2 , December 1987 , pp. 155 - 159
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Findeisen, P.. Die Charakterisierung der Normalverteilung nach GauB. Metrika, 29 (1982), 55–64.CrossRefGoogle Scholar
2.Oxtoby, J. C.. Measure and Category. 2nd Ed. (Springer, New York, 1980).CrossRefGoogle Scholar
3.Roberts, A. W. and Varberg, D. E.. Convex Functions (Acad. Press, New York and London, 1973).Google Scholar
4.Teicher, H.. Maximum likelihood characterization of distributions. Ann. Math. Statist., 32 (1961), 1214–1222.CrossRefGoogle Scholar