Article contents
WEIGHTED INEQUALITIES FOR MARTINGALE TRANSFORMS AND STOCHASTIC INTEGRALS
Published online by Cambridge University Press: 20 February 2017
Abstract
The paper is devoted to the study of Fefferman–Stein inequalities for stochastic integrals. If 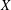 $X$ is a martingale,
$X$ is a martingale, 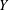 $Y$ is the stochastic integral, with respect to
$Y$ is the stochastic integral, with respect to 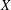 $X$, of some predictable process taking values in
$X$, of some predictable process taking values in 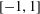 $[-1,1]$, then for any weight
$[-1,1]$, then for any weight 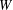 $W$ belonging to the class
$W$ belonging to the class 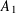 $A_{1}$ we have the estimates
$A_{1}$ we have the estimates 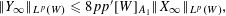 $\Vert Y_{\infty }\Vert _{L^{p}(W)}\leqslant 8pp^{\prime }[W]_{A_{1}}\Vert X_{\infty }\Vert _{L^{p}(W)},$
$\Vert Y_{\infty }\Vert _{L^{p}(W)}\leqslant 8pp^{\prime }[W]_{A_{1}}\Vert X_{\infty }\Vert _{L^{p}(W)},$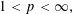 $1<p<\infty ,$ and
$1<p<\infty ,$ and 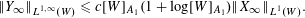 $\Vert Y_{\infty }\Vert _{L^{1,\infty }(W)}\leqslant c[W]_{A_{1}}(1+\log [W]_{A_{1}})\Vert X_{\infty }\Vert _{L^{1}(W)}.$ The proofs rest on the Bellman function method: the inequalities are deduced from the existence of certain special functions, enjoying appropriate majorization and concavity. As an application, related statements for Haar multipliers are indicated. The above estimates can be regarded as probabilistic counterparts of the recent results of Lerner, Ombrosi and Pérez concerning singular integral operators.
$\Vert Y_{\infty }\Vert _{L^{1,\infty }(W)}\leqslant c[W]_{A_{1}}(1+\log [W]_{A_{1}})\Vert X_{\infty }\Vert _{L^{1}(W)}.$ The proofs rest on the Bellman function method: the inequalities are deduced from the existence of certain special functions, enjoying appropriate majorization and concavity. As an application, related statements for Haar multipliers are indicated. The above estimates can be regarded as probabilistic counterparts of the recent results of Lerner, Ombrosi and Pérez concerning singular integral operators.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2017
References
- 2
- Cited by


