Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T08:06:38.652Z Has data issue: false hasContentIssue false
  • English
  • Français

The Upper-Bound Theorem for Families of Boxes in ℝd

Part of: General convexity

Published online by Cambridge University Press:  21 December 2009

Jürgen Eckhoff
Jürgen Eckhoff
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT, England.
Get access

Abstract

Let 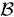be a family of axis-aligned parallelotopes, or boxes, in ℝd. Denote by fk (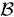) the number of subfamilies of 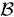of size k + 1 with non-empty intersection. In an earlier paper, the author proved that, if f0 (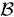) = n and fr(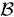) = 0, then fk(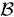) ≤ fk(n, d, r) for k = 1,…,r − 1, where fk(n, d, r) is some explicitly given number. The result is best possible for all k. Here it is shown that, if equality is attained for some such k, then equality is attained for each such k.

MSC classification

Secondary: 52A37: Other problems of combinatorial convexity
Type
Research Article
Information
Mathematika , Volume 54 , Issue 1-2 , December 2007 , pp. 25 - 34
Copyright
Copyright © University College London 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alon, N. and Kalai, G., A simple proof of the upper bound theorem. European J. Combin. 6 (1985), 211–214.CrossRefGoogle Scholar
2Billera, L. J. and Björner, A., Face numbers of polytopes and complexes. In Handbook of Discrete and Computational Geometry (ed. Goodman, J. E. and O'Rourke, J.), CRC Press (2004), 291–315.Google Scholar
3Eckhoff, J., An upper-bound theorem for families of convex sets. Geom. Dedicata 19 (1985), 217–227.CrossRefGoogle Scholar
4Eckhoff, J., Intersection properties of boxes, I: an upper-bound theorem. Israel J. Math. 62 (1988), 283–301.CrossRefGoogle Scholar
5Eckhoff, J., Intersection properties of boxes, II: extremal families. Israel J. Math. 73 (1991), 129–149.CrossRefGoogle Scholar
6Eckhoff, J., Extremal interval graphs. J. Graph Theory 17 (1993), 117–127.CrossRefGoogle Scholar
7Eckhoff, J., Helly, Radon and Carathéodory type theorems. In Handbook of Convex Geometry (ed. Gruber, P. M. and Wills, J. M.), North-Holland (1993), 389–448.CrossRefGoogle Scholar
8Eckhoff, J., Generalized binomial coefficients, colored simplicial complexes, and tight inequalities between elementary symmetric functions of integers. Amer. Math. Monthly (submitted).Google Scholar
9Frohmader, A., Face vectors of flag complexes. Manuscript, University of Washington, May 2006.Google Scholar
10Kalai, G., Intersection patterns of convex sets. Israel J. Math. 48 (1984), 161–174.CrossRefGoogle Scholar
11Kalai, G., Characterization of f−vectors of families of convex sets in R d, I: necessity of Eckhoff's conditions. Israel J. Math. 48 (1984), 175–195.CrossRefGoogle Scholar
12Kalai, G., Characterization of f-vectors of families of convex sets in R d, II: sufficiency of Eckhoff's conditions. J. Combin. Theory Ser. A 41 (1986), 167–188.CrossRefGoogle Scholar
13McMullen, P., The maximum numbers of faces of a convex polytope. Mathematika 17 (1970), 179–184.CrossRefGoogle Scholar