Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T05:02:31.108Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SQUARE TERMS IN GENERALIZED LUCAS SEQUENCES

Part of: Sequences and sets

Published online by Cambridge University Press:  19 December 2013

Zafer Şi̇ar  and
Refi̇k Keski̇n
Zafer Şi̇ar
Affiliation:
Bilecik Şeyh Edebali University, Faculty of Science and Arts, Department of Mathematics, Bilecik/TURKEY email [email protected]
Refi̇k Keski̇n*
Affiliation:
Sakarya University, Faculty of Science and Arts, Department of Mathematics, Sakarya/TURKEY
*
[email protected]
Get access

Abstract

Let 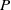$P$ and 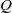$Q$ be non-zero integers. The generalized Fibonacci sequence 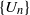$\{ {U}_{n} \} $ and Lucas sequence 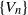$\{ {V}_{n} \} $ are defined by ${U}_{0} = 0$, 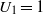${U}_{1} = 1$ and 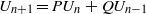${U}_{n+ 1} = P{U}_{n} + Q{U}_{n- 1} $ for 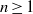$n\geq 1$ and 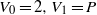${V}_{0} = 2, {V}_{1} = P$ and 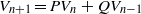${V}_{n+ 1} = P{V}_{n} + Q{V}_{n- 1} $ for 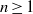$n\geq 1$, respectively. In this paper, we assume that 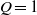$Q= 1$. Firstly, we determine indices $n$ such that 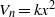${V}_{n} = k{x}^{2} $ when 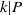$k\vert P$ and 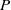$P$ is odd. Then, when $P$ is odd, we show that there are no solutions of the equation 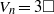${V}_{n} = 3\square $ for 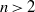$n\gt 2$. Moreover, we show that the equation 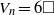${V}_{n} = 6\square $ has no solution when 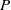$P$ is odd. Lastly, we consider the equations 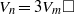${V}_{n} = 3{V}_{m} \square $ and 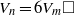${V}_{n} = 6{V}_{m} \square $. It has been shown that the equation 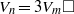${V}_{n} = 3{V}_{m} \square $ has a solution when 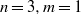$n= 3, m= 1$, and $P$ is odd. It has also been shown that the equation 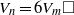${V}_{n} = 6{V}_{m} \square $ has a solution only when 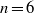$n= 6$. We also solve the equations 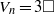${V}_{n} = 3\square $ and 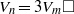${V}_{n} = 3{V}_{m} \square $ under some assumptions when 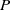$P$ is even.

MSC classification

Secondary: 11B37: Recurrences 11B39: Fibonacci and Lucas numbers and polynomials and generalizations
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 85 - 100
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antoniadis, J. A., Fibonacci and Lucas numbers of the form $3{z}^{2} \pm 1$. Fibonacci Quart. 23 (1985), 300–307.Google Scholar
Cohn, J. H. E., Square Fibonacci numbers, etc. Fibonacci Quart. 2.2 (1964), 109–113.Google Scholar
Cohn, J. H. E., Eight Diophantine equations. Proc. Lond. Math. Soc. 16 (1966), 153–166.Google Scholar
Cohn, J. H. E., Five Diophantine equations. Math. Scand. 21 (1967), 61–70.Google Scholar
Cohn, J. H. E., Squares in some recurrent sequences. Pacific J. Math. 41 (1972), 631–646.Google Scholar
Kagawa, T. and Terai, N., Squares in Lucas sequences and some Diophantine equations. Manuscripta Math. 96 (1998), 195–202.Google Scholar
Kalman, D. and Mena, R., The Fibonacci numbers—exposed. Mathematics Magazine 76 (2003), 167–181.Google Scholar
Keskin, R. and Yosma, Z., On Fibonacci and Lucas numbers of the form $c{x}^{2} $. J. Integer Seq. 14 (2011), article no. 11.9.3.Google Scholar
Ljunggren, W., Zur Theorie der Gleichung ${x}^{2} + 1= D{y}^{4} $. Det Norske Vid. Akad. Avh. I 5 (1942), 333–341.Google Scholar
McDaniel, W. L., The g.c.d. in Lucas sequences and Lehmer number sequences. Fibonacci Quart. 29 (1991), 24–30.Google Scholar
Mignotte, M. and Pethő, A., Sur les carrés dans certaines suites de Lucas. J. Théor. Nombres Bordeaux 5 (2) (1993), 333–341.Google Scholar
Muskat, J. B., Generalized Fibonacci and Lucas sequences and rootfinding methods. Math. Comp. 61 (1993), 365–372.CrossRefGoogle Scholar
Nakamula, K. and Pethő, A., Squares in binary recurrence sequences. In Number Theory: Diophantine, Computational and Algebraic Aspects (eds Győry, K., Pethő, A. and Sós, V. T.),de Gruyter (Berlin, 1998), 409–421.Google Scholar
Rabinowitz, S., Algorithmic manipulation of Fibonacci identities. Appl. Fibonacci Numb. 6 (1996), 389–408.CrossRefGoogle Scholar
Ribenboim, P. and McDaniel, W. L., The square terms in Lucas sequences. J. Number Theory 58 (1996), 104–123.Google Scholar
Ribenboim, P. and McDaniel, W. L., Squares in Lucas sequences having an even first parameter. Colloq. Math. 78 (1998), 29–34.Google Scholar
Ribenboim, P., My Numbers, My Friends, Springer (New York, 2000).Google Scholar
Ribenboim, P. and McDaniel, W. L., On Lucas sequence terms of the form $k{x}^{2} $. In Number Theory: Proceedings of the Turku Symposium on Number Theory in Memory of Kustaa Inkeri (Turku, 1999), de Gruyter (Berlin, 2001), 293–303.Google Scholar
Shorey, T. N. and Stewart, C. L., On the Diophantine equation $a{x}^{2t} + b{x}^{t} y+ c{y}^{2} = 1$ and pure powers in recurrence sequences. Math. Scand. 52 (1983), 24–36.Google Scholar
Şiar, Z. and Keskin, R., Some new identities concerning generalized Fibonacci and Lucas numbers. Hacet. J. Math. Stat. 42 (3) (2013), 211–222.Google Scholar
Walker, D. T., On the Diophantine equation $m{X}^{2} - n{Y}^{2} = \pm 1$. Amer. Math. Monthly 74 (1967), 504–513.Google Scholar