Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T05:06:18.688Z Has data issue: false hasContentIssue false
  • English
  • Français

A SMALL VALUE ESTIMATE FOR 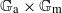$\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  01 February 2013

Damien Roy
Damien Roy*
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 585 King Edward, Ottawa K1N 6N5, Canada (email: [email protected])
Get access

Abstract

A small value estimate is a statement providing necessary conditions for the existence of certain sequences of non-zero polynomials with integer coefficients taking small values at points of an algebraic group. Such statements are desirable for applications to transcendental number theory to analyze the outcome of the construction of an auxiliary function. In this paper, we present a result of this type for the product 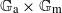$ \mathbb {G}_{\mathrm {a}}\times \mathbb {G}_{\mathrm {m}}$ whose underlying group of complex points is $\mathbb {C}\times \mathbb {C}^{*}$. It shows that if a certain sequence of non-zero polynomials in 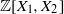$ \mathbb {Z}[X_1,X_2]$ takes small values at a point $(\xi ,\eta )$ together with their first derivatives with respect to the invariant derivation $\partial /\partial X_1 + X_2 (\partial /\partial X_2)$, then both 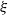$\xi $ and $\eta $ are algebraic over 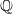$\mathbb {Q}$. The precise statement involves growth conditions on the degree and norm of these polynomials as well as on the absolute values of their derivatives. It improves on a direct application of Philippon’s criterion for algebraic independence and compares favorably with constructions coming from Dirichlet’s box principle.

MSC classification

Secondary: 11J85: Algebraic independence; Gel'fond's method 11J81: Transcendence (general theory)
Type
Research Article
Information
Mathematika , Volume 59 , Issue 2 , July 2013 , pp. 333 - 363
Copyright
Copyright © 2013 University College London 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Brownawell, W. D. and Masser, D. W., Multiplicity estimates for analytic functions II. Duke Math. J. 47 (1980), 273–295.CrossRefGoogle Scholar
[2]Fischler, S., Interpolation on algebraic groups. Compos. Math. 141 (2005), 907–925.CrossRefGoogle Scholar
[3]Laurent, M. and Roy, D., Criteria of algebraic independence with multiplicities and approximation by hypersurfaces. J. Reine Angew. Math. 536 (2001), 65–114.Google Scholar
[4]Mahler, K., On a class of entire functions. Acta Math. Acad. Sci. Hungar. 18 (1967), 83–96.CrossRefGoogle Scholar
[5]Masser, D. W., On polynomials and exponential polynomials in several complex variables. Invent. Math. 63 (1981), 81–95.CrossRefGoogle Scholar
[6]Nesterenko, Yu. V., Estimates for the orders of zeros of functions of a certain class and their applications in the theory of transcendental numbers. Izv. Akad. Nauk SSSR Ser. Mat. 41 (1977), 253–284; English transl. in Math. USSR Izv. 11 (1977), 239–270.Google Scholar
[7]Nesterenko, Yu. V., On algebraic independence of algebraic powers of algebraic numbers. Mat. Sb. 123 (1984), 435–459; English transl. in Math. USSR Sb. 51 (1985), 429–454.Google Scholar
[8]Philippon, P., Critères pour l’indépendance algébrique. Publ. Math. Inst. Hautes Études Sci. 64 (1986), 5–52.CrossRefGoogle Scholar
[9]Philippon, P., Quatre exposés sur la théorie de l’élimination. Quelques aspects de la théorie de l’élimination, prétirage no. 94-25, Laboratoire de mathématiques discrètes, CNRS, 1994, 2–46. Available at http://www.math.jussieu.fr/∼pph/DEACIRM93.pdf.Google Scholar
[10]Rémond, G., Élimination multiprojective (Chapter 5) and Géométrie diophantienne multiprojective (Chapter 7). In Introduction to Algebraic Independence Theory (Lecture Notes in Mathematics 1752) (eds Philippon, P. and Nesterenko, Yu.), Springer (New York, 2001).Google Scholar
[11]Roy, D., An arithmetic criterion for the values of the exponential function. Acta Arith. 97 (2001), 183–194.CrossRefGoogle Scholar
[12]Roy, D., Interpolation formulas and auxiliary functions. J. Number Theory 94 (2002), 248–285.CrossRefGoogle Scholar
[13]Roy, D., Small value estimates for the multiplicative group. Acta Arith. 135 (2008), 357–393.CrossRefGoogle Scholar
[14]Roy, D., Small value estimates for the additive group. Int. J. Number Theory 6 (2010), 919–956.CrossRefGoogle Scholar
[15]Tijdeman, R., An auxiliary result in the theory of transcendental numbers. J. Number Theory 5 (1973), 80–94.CrossRefGoogle Scholar