Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T04:25:52.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous Diophantine Approximation

Published online by Cambridge University Press:  26 February 2010

H. Davenport
H. Davenport
Affiliation:
University College, London, W.C.I.
Get access

Extract

It is well known that every irrational number θ possesses an infinity of rational approximations p/q satisfying

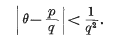
It is also well known that there is a wide class of irrational numbers which admit of no approximations which are essentially better, namely those θ whose continued fractions have bounded partial quotients. For any such θ there is a positive number c such that all rational approximations satisfy

Type
Research Article
Information
Mathematika , Volume 1 , Issue 1 , June 1954 , pp. 51 - 72
Copyright
Copyright © University College London 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page note 51 * Math. Annalen, 83 (1921), 77à84.

page note 52 * This is a special ease of the “Uebertragungsprinzip”: see Koksma, , Diophantische Approximationen (Berlin, 1936), ch. 5, §1.Google Scholar

page note 53 * The field k is the cubic subfleld of the field of the 7th roots of unity, and α = 2 cos 2π/7, β = 2 cos 4π/7, γ = 2 cos 8π/7.

page note 53 † The field K is the cubic subfield of the field of the 7th roots of unity, and A = - 2 cos 8α/9, B = – 2 cos 4α/9, r = - 2 cos 2π/9.

page note 66 * An alternative method is to use the formulae of §6. We can express τn+1(1+p n+1), τn+1q n+1, τn+1r n+1 linearly in terms of 1+p n, q n, r n as in (42), (43), (44). The inverse formulae lead to the same expressions for qn and r n as those obtained above.