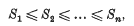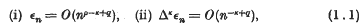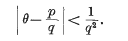Research Article
History of Science and Psychology of Invention
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-3
-
- Article
- Export citation
A simple proof of η(— 1/τ)= η(τ)√τ/i
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 4
-
- Article
- Export citation
The stability of viscous flow between rotating cylinders
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 5-13
-
- Article
- Export citation
The minimal points of a positive definite quadratic form
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 14-17
-
- Article
- Export citation
The Green's function of an elastic plate
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-23
-
- Article
- Export citation
On convergence and summability factors in a sequence
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-44
-
- Article
- Export citation
The stability of an incompressible electrically conducting fluid rotating about an axis when current flows parallel to the axis
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-50
-
- Article
- Export citation
Simultaneous Diophantine Approximation
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-72
-
- Article
- Export citation
Front matter
MTK volume 1 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
-
- Article
-
- You have access
- Export citation

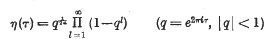
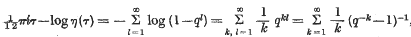
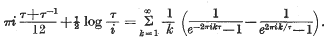

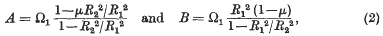

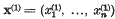 be a point at which this value is attained. Let
be a point at which this value is attained. Let