Published online by Cambridge University Press: 28 November 2011
In 1946 Erdős asked for the maximum number of unit distances, u(n), among n points in the plane. He showed that u(n)>n1+c/log log n and conjectured that this was the true magnitude. The best known upper bound is u(n)<cn4/3, due to Spencer, Szemerédi and Trotter. We show that the upper bound 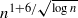 holds if we only consider unit distances with rational angle, by which we mean that the line through the pair of points makes a rational angle in degrees with the x-axis. Using an algebraic theorem of Mann we get a uniform bound on the number of paths between two fixed vertices in the unit distance graph, giving a contradiction if there are too many unit distances with rational angle. This bound holds if we consider rational distances instead of unit distances as long as there are no three points on a line. A superlinear lower bound is given, due to Erdős and Purdy. If we have at most nα points on a line then we get the bound O(n1+α) or
holds if we only consider unit distances with rational angle, by which we mean that the line through the pair of points makes a rational angle in degrees with the x-axis. Using an algebraic theorem of Mann we get a uniform bound on the number of paths between two fixed vertices in the unit distance graph, giving a contradiction if there are too many unit distances with rational angle. This bound holds if we consider rational distances instead of unit distances as long as there are no three points on a line. A superlinear lower bound is given, due to Erdős and Purdy. If we have at most nα points on a line then we get the bound O(n1+α) or 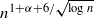 for the number of rational distances with rational angle depending on whether α≥1/2 or α<1/2 respectively.
for the number of rational distances with rational angle depending on whether α≥1/2 or α<1/2 respectively.