Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T16:11:23.451Z Has data issue: false hasContentIssue false
  • English
  • Français

Piece-wise closed functions and almost discretely σ-decomposable families

Part of: Maps and general types of spaces defined by maps

Published online by Cambridge University Press:  26 February 2010

R. W. Hansell ,
J. E. Jayne  and
C. A. Rogers
R. W. Hansell
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06268, U.S.A
J. E. Jayne
Affiliation:
Department of Mathematics, University College London, Gower Street, London. WCIE 6BT
C. A. Rogers
Affiliation:
Department of Mathematics, University College London, Gower Street, London. WC1E 6BT
Get access

Extract

In [8,9] Jayne and Rogers studied piece-wise closed maps and ℱσ maps between metric spaces. A map f of a metric space X into a metric space Y is said to be an ℱσ map if: (a) f maps ℱσ-sets in X to ℱσ-sets in Y; and (b) f1 maps ℱσ-sets in Y back to ℱσ-sets in X. A map fof a metric space X into a metric space Y is said to be piece-wise closed if:it is possible to find a sequence X1, X2,… of closed sets in X, with 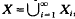with each setf(Xi), i ≥ 1, closed in Y, and with the restriction offto each Xi, a closed map (i.e., a continuous map that maps closed sets to closed sets).

MSC classification

Secondary: 54C50: Special sets defined by functions
Type
Research Article
Information
Mathematika , Volume 32 , Issue 2 , December 1985 , pp. 229 - 247
Copyright
Copyright © University College London 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alexandrov, P. S., Sur la puissance des ensembles mesurables B. C. R. Acad. Sci. Paris, 162 (1916), 323–325.Google Scholar
2.Alexandrov, P. S.. Über abzählbar-fache offene Abbildungen. Dokl. Akad. Nauk SSSR, 6(13) (1936), 295–299.Google Scholar
3.El'kin, A. G.. A-sets in complete metric spaces. Dokl. Akad. Nauk SSSR, 175 (1967), 517–520 (= Soviet Math. Dokl., 8 (1967), 874–877.).Google Scholar
4.Fleissner, W. G.. An axiom for nonseparable Borel theory. Trans. Amer. Math. Soc., 251 (1979), 309–328.CrossRefGoogle Scholar
5.Hansell, R. W.. Borel measurable mappings for nonseparable metric spaces. Trans. Amer. Math. Soc., 161 (1971), 145–169.CrossRefGoogle Scholar
6.Hansell, R. W.. On characterizing non-seprable analytic and extended Borel sets as types of continuous images. Proc. London Math. Soc., 28 (1974), 683–699.CrossRefGoogle Scholar
7.Jayne, J. E. and Rogers, C. A.. Fonctions et isomorphismes boreliéns du premier niveau. C. R. Acad. Sci. Paris Sér. A, 291 (1980), 351–354.Google Scholar
8.Jayne, J. E. and Rogers, C. A.. Fonctions fermées en partie. C. R. Acad. Sci. Paris Sér. A, 291 (1980), 667–670.Google Scholar
9.Jayne, J. E. and Rogers, C. A.. Piece-wise closed functions. Math. Ann., 255 (1981), 499–518 and Corrigendum, 267 (1984), 143.CrossRefGoogle Scholar
10.Jayne, J. E. and Rogers, C. A.. First level Borel functions and isomorphisms. J. Math. Pures Appl., 61 (1982), 177–205.Google Scholar
11.Jayne, J. E. and Rogers, C. A.. The invariance of the absolute Borel classes. In Convex Analysis and Optimization, Research Notes in Math., No. 57, pp. 118–151 (Pitman Books Ltd., London, 1982).Google Scholar
12.Kaniewski, J. and Pol, R.. Borel measurable selectors for compact-valued mappings in the non-separable case. Bull. Acad. Polon. Sci., 23 (1975), 1043–1050.Google Scholar
13.Michael, E.. On maps related to σ-locally finite and σ-discrete collections of sets. Pacific J. Math., 98 (1982), 139–152.CrossRefGoogle Scholar
14.Pol, R.. Note on decompositions of metrizable spaces I. Fund. Math., 95 (1977), 95–103.CrossRefGoogle Scholar
15.Pol, R.. Note on decompositions of metrizable spaces II. Fund Math., 100 (1978), 129–143.CrossRefGoogle Scholar
16.Rogers, C. A., Jayne, J. E. and Dellacherie, C. and Topsøe, F. and Hoffmann-Jørgensen, J., Martin, D. A. and Kechris, A. S. and Stone, A. H.. Analytic Sets (Academic Press, London 1980).Google Scholar
17.Stone, A. H.. Non-separable Borel sets. Dissertationes Math. (Rozprawy Mat.), 28 (1962), 1–40.Google Scholar
18.Stone, A. H.. On tr-discreteness and Borel isomorphism. Amer. J. Math., 85 (1963), 655–666.CrossRefGoogle Scholar