Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T05:50:15.242Z Has data issue: false hasContentIssue false
  • English
  • Français

On the status of the uncoupled approximation within quasistatic thermoelasticity

Published online by Cambridge University Press:  26 February 2010

W. A. Day
W. A. Day
Affiliation:
Hertford College, Oxford.
Get access

Extract

We consider a body which occupies the open, bounded, regular region B, whose boundary is ∂B and whose closure is 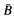. We denote by da the element of surface area, by dυ the element of volume, and by n the outward unit normal. We suppose the behaviour of the body to be described by the equations of the quasi-static theory of homogeneous and isotropic thermoelasticity. These equations, which are obtained from the equations of the dynamical theory (see, for example, Carlson [1], Chadwick [2] or Boley and Weiner [3]) by omitting the inertial term pű from the right-hand side of the equation of motion (4), are:

Type
Research Article
Information
Mathematika , Volume 28 , Issue 2 , December 1981 , pp. 286 - 294
Copyright
Copyright © University College London 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Carlson, D. E.. “Linear Thermoelasticity”, The Encyclopedia of Physics, Vol. VIa/2 (Springer, 1972).Google Scholar
2.Chadwick, P.. “Thermoelasticity. The Dynamical Theory”, Progress in Solid Mechanics, Vol. 1 (North-Holland, 1960).Google Scholar
3.Boley, B. A. and Weiner, J. H.. Theory of Thermal Stresses (Wiley, 1960).Google Scholar
4.Day, W. A.. “Justification of the uncoupled and quasi-static approximations in a problem of dynamic thermoelasticity”, Arch. Rational Mech. Anal., to appear.Google Scholar
5.Day, W. A.. “Further justification of the uncoupled and quasi-static approximations in thermoelasticity”, Arch. Rational Mech. Anal, to appear.Google Scholar
6.Sigillito, V. G.. Explicit A Priori Inequalities with Applications to Boundary Value Problems (Pitman, 1977).Google Scholar