Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T05:15:53.537Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NILPOTENT SECTION CONJECTURE FOR FINITE GROUP ACTIONS ON CURVES

Part of: Algebraic groups Curves

Published online by Cambridge University Press:  13 December 2013

Ambrus Pál
Ambrus Pál*
Affiliation:
Department of Mathematics, 180 Queen’s Gate, Imperial College, London, SW7 2AZ,U.K. email [email protected]
Get access

Abstract

We give a new, geometric proof of the section conjecture for fixed points of finite group actions on projective curves of positive genus defined over the field of complex numbers, as well as its natural nilpotent analogue. As a part of our investigations we give an explicit description of the abelianised section map for groups of prime order in this setting. We also show a version of the 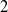$2$-nilpotent section conjecture.

MSC classification

Secondary: 14H30: Coverings, fundamental group 14L30: Group actions on varieties or schemes (quotients)
Type
Research Article
Information
Mathematika , Volume 60 , Issue 1 , January 2014 , pp. 183 - 200
Copyright
Copyright © University College London 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, M. and Mazur, B., Étale homotopy (Lecture Notes in Mathematics 100), Springer (Berlin-Heidelberg, 1969).Google Scholar
Hartshorne, R., Algebraic geometry (Graduate Texts in Mathematics 52), Springer (1977).Google Scholar
Pál, A., The real section conjecture and Smith’s fixed point theorem for pro-spaces. J. Lond. Math. Soc. 83 (2011), 353–367.Google Scholar
Serre, J.-P., Cohomologie Galoisienne, 5th edn (Lecture Notes in Mathematics 5), Springer (Berlin-Heidelberg, 1997).Google Scholar
Tamagawa, A., The Grothendieck conjecture for affine curves. Compositio Math. 109 (1997), 135–194.Google Scholar
Wickelgren, K., 2-nilpotent real section conjecture. Math. Ann., to appear, arXiv:1006.0265.Google Scholar
Zarkhin, Yu. G., Noncommutative cohomology and Mumford groups. Mat. Zametki 15 (1974), 415–419.Google Scholar