Article contents
On the convolution of Hecke L-functions
Published online by Cambridge University Press: 26 February 2010
Extract
§1. Let k be an algebraic number field of finite degree over the field Q of rational numbers and Ki be an extension of k of degree (Ki:k) = ni, i = 1,2. We choose a Hecke Grössencharakter Xi in Ki and consider the L-function
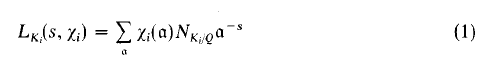
associated with Xi see [1, 2]. It is known to be a meromorphic function on the whole complex plane. We are interested here in the properties of the convolution of functions LK1, LK2 over k defined by

where
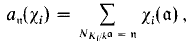
and a (and n) run over integral ideals of Ki (and k), whose norm NKi/k a is equal to n. The function (2) is sometimes called the “scalar product of the Hecke L-functions” «3—11». The object of the paper is the following theorem.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1980
References
- 3
- Cited by


