The minimal points of a positive definite quadratic form

Extract

Let q(x₁; …, x_n) be a positive definite quadratic form in n variables with real coefficients. Minkowski defined the successive minima of q as follows. Let S₁ denote the least value assumed by q for integers x₁ …, x_n, not all zero, and let 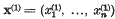be a point at which this value is attained. Let S₂ denote the least value assumed by q at integral points which are not multiples of x⁽¹⁾, and let x⁽²⁾ be such a point at which this value is attained. Let S₃ be the least value of q at integral points which are not linearly dependent on x⁽¹⁾ and x⁽²⁾, and so on. We have

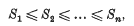
and it is easy to see that these numbers are uniquely defined, even though there may be several choices for the points x⁽¹⁾, …, x⁽ⁿ⁾. The determinant N of the coordinates of the points x⁽¹⁾, …, x⁽ⁿ⁾ is a non-zero integer. We denote by N (q) the least value of this integer (taken positively) for all permissible choices of the n minimal points, and by N′(q) its greatest value. Plainly N(q) and N′(q) are arithmetical invariants of q, that is, they are the same for two forms which are equivalent under a linear substitution with integral coefficients and determinant ±1.