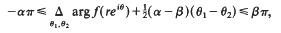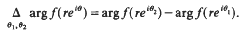Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jahangiri, M.
1989.
On the gap between two classes of analytic functions.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 99,
Issue. 2,
p.
123.
Jahangiri, Massoud
1989.
Weighted convolutions of certain polynomials.
Bulletin of the Australian Mathematical Society,
Vol. 40,
Issue. 3,
p.
397.
Jahangiri, Jay M.
Morgan, Chris
and
Suffridge, Ted J.
2001.
Construction of close-to-convex harmonic polynomials.
Complex Variables, Theory and Application: An International Journal,
Vol. 45,
Issue. 4,
p.
319.
Jahangiri, Jay M.
2007.
Generalized bounded boundary turning functions.
Applied Mathematics and Computation,
Vol. 187,
Issue. 1,
p.
215.
Lamprecht, Martin
2011.
Interspersion in Suffridge’s Polynomial Theory.
Computational Methods and Function Theory,
Vol. 11,
Issue. 1,
p.
325.
Jahangiri, Jay M.
and
Ponnusamy, S.
2012.
Applications of subordination to functions with bounded boundary rotation.
Archiv der Mathematik,
Vol. 98,
Issue. 2,
p.
173.
Ignaciuk, Sz.
and
Parol, M.
2020.
Zeros of complex polynomials and Kaplan classes.
Analysis Mathematica,
Vol. 46,
Issue. 4,
p.
769.
Ignaciuk, Szymon
and
Parol, Maciej
2024.
A Gap Condition for the Zeros and Singularities of a Certain Class of Products.
Complex Analysis and Operator Theory,
Vol. 18,
Issue. 5,