Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marquezino, Franklin de Lima
Portugal, Renato
and
Boettcher, Stefan
2013.
Spatial search algorithms on Hanoi networks.
Physical Review A,
Vol. 87,
Issue. 1,
Portugal, Renato
2013.
Quantum Walks and Search Algorithms.
p.
145.
Portugal, Renato
2016.
Establishing the equivalence between Szegedy’s and coined quantum walks using the staggered model.
Quantum Information Processing,
Vol. 15,
Issue. 4,
p.
1387.
Matsue, Kaname
Ogurisu, Osamu
and
Segawa, Etsuo
2016.
Quantum walks on simplicial complexes.
Quantum Information Processing,
Vol. 15,
Issue. 5,
p.
1865.
Chagas, Bruno
Portugal, Renato
Boettcher, Stefan
and
Segawa, Etsuo
2018.
Staggered quantum walk on hexagonal lattices.
Physical Review A,
Vol. 98,
Issue. 5,
Matsue, Kaname
Ogurisu, Osamu
and
Segawa, Etsuo
2018.
Quantum search on simplicial complexes.
Quantum Studies: Mathematics and Foundations,
Vol. 5,
Issue. 4,
p.
551.
Arrighi, Pablo
Di Molfetta, Giuseppe
Márquez-Martín, Iván
and
Pérez, Armando
2018.
Dirac equation as a quantum walk over the honeycomb and triangular lattices.
Physical Review A,
Vol. 97,
Issue. 6,
Giri, Pulak Ranjan
and
Korepin, Vladimir
2019.
Quantum search on Hanoi network.
International Journal of Quantum Information,
Vol. 17,
Issue. 07,
p.
1950060.
Osawa, Shuto
Simon, David S.
and
Sergienko, Alexander V.
2019.
Directionally-Unbiased Unitary Optical Devices in Discrete-Time Quantum Walks.
Entropy,
Vol. 21,
Issue. 9,
p.
853.
Osawa, Shuto
Simon, David S.
Sergienko, Alexander V.
and
Deacon, Keith S.
2019.
Investigation of directional and directionally-unbiased devices in linear optics for quantum walk applications.
p.
12.
Benedetti, Claudia
Tamascelli, Dario
Paris, Matteo G.A.
and
Crespi, Andrea
2021.
Quantum Spatial Search in Two-Dimensional Waveguide Arrays.
Physical Review Applied,
Vol. 16,
Issue. 5,
Segawa, Etsuo
and
Yoshie, Yusuke
2021.
Quantum search of matching on signed graphs.
Quantum Information Processing,
Vol. 20,
Issue. 5,
Nahimovs, Nikolajs
and
Santos, Raqueline A M
2021.
Lackadaisical quantum walks on 2D grids with multiple marked vertices.
Journal of Physics A: Mathematical and Theoretical,
Vol. 54,
Issue. 41,
p.
415301.
Yoshie, Yusuke
and
Yoshino, Kiyoto
2022.
A quantum searching model finding one of the edges of a subgraph in a complete graph.
Quantum Information Processing,
Vol. 21,
Issue. 6,
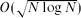 .
.