Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T01:34:33.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Separating minimal valuations, point-continuous valuations, and continuous valuations

Published online by Cambridge University Press:  07 December 2021

Jean Goubault-Larrecq Open the ORCID record for Jean Goubault-Larrecq [Opens in a new window]  and
Xiaodong Jia Open the ORCID record for Xiaodong Jia [Opens in a new window]
Jean Goubault-Larrecq
Affiliation:
Université Paris-Saclay, CNRS, ENS Paris-Saclay, Laboratoire Méthodes Formelles, 91190, Gif-sur-Yvette, France
Xiaodong Jia*
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan, 410082, China
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give two concrete examples of continuous valuations on dcpo’s to separate minimal valuations, point-continuous valuations, and continuous valuations:

  1. (1) Let 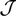${\mathcal J}$ be the Johnstone’s non-sober dcpo, and μ be the continuous valuation on 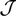${\mathcal J}$ with μ(U)=1 for nonempty Scott opens U and μ(U)=0 for 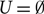$U=\emptyset$. Then, μ is a point-continuous valuation on 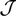${\mathcal J}$ that is not minimal.

  2. (2) Lebesgue measure extends to a measure on the Sorgenfrey line 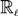$\mathbb{R}_\ell$. Its restriction to the open subsets of 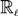$\mathbb{R}_\ell$ is a continuous valuation λ. Then, its image valuation 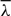$\overline\lambda$ through the embedding of 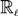$\mathbb{R}_\ell$ into its Smyth powerdomain 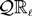$\mathcal{Q}\mathbb{R}_\ell$ in the Scott topology is a continuous valuation that is not point-continuous.

We believe that our construction 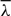$\overline\lambda$ might be useful in giving counterexamples displaying the failure of the general Fubini-type equations on dcpo’s.

Keywords

Minimal valuationspoint-continuous valuationscontinuous valuationsFubini equations
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Issue 6 , June 2021 , pp. 614 - 632
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramsky, S. and Jung, A. (1994). Domain theory. In: Abramsky, S., Gabbay, D. M. and Maibaum, T. S. E. (eds.), Semantic Structures, vol. 3. Handbook of Logic in Computer Science. Clarendon Press, 1–168.Google Scholar
Adamski, W. (1977). τ -smooth Borel measures on topological spaces. Mathematische Nachrichten 78 97–107.CrossRefGoogle Scholar
Alvarez-Manilla, M., Edalat, A. and Saheb-Djahromi, N. (2000). An extension result for continuous valuations. Journal of the London Mathematical Society 61 629–640.CrossRefGoogle Scholar
Bouziad, A. (1996). Borel measures in consonant spaces. Topology and Its Applications 70 125–138.CrossRefGoogle Scholar
Costantini, C. and Watson, S. (1996). On the dissonance of some metrizable spaces. Topology and Its Applications 84 259–268.CrossRefGoogle Scholar
Gierz, G., Hofmann, K. H., Keimel, K., Lawson, J. D., Mislove, M. and Scott, D. S. (2003). Continuous Lattices and Domains, vol. 93. Encyclopedia of Mathematics and its Applications. Cambridge University Press.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2015). Full abstraction for non-deterministic and probabilistic extensions of PCF I — The angelic cases. Journal of Logical and Algebraic Methods in Programming 84 (1) 155–184.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2013). Non-Hausdorff Topology and Domain Theory, vol. 22. New Mathematical Monographs. Cambridge University Press.CrossRefGoogle Scholar
Goubault-Larrecq, J. (2021). Products and projective limits of continuous valuations on T0 spaces. Accepted for Publication in “Mathematical Structure in Computer Science”.CrossRefGoogle Scholar
He, Q., Li, G., Xi, X. and Zhao, D. (2019). Some results on poset models consisting of compact saturated subsets. Electronic Notes in Theoretical Computer Science 345 77–85. Proceedings of the 8th International Symposium of Domain Theory (ISDT 2019), Jung, A., Li, Q., Xu, L. and Zhang, G.-Q. (eds).CrossRefGoogle Scholar
Heckmann, R. (1995). Spaces of valuations. Technical Report A 09/95, FB 14 Informatik, Universität des Saarlandes, 66041 Saarbrücken, Germany.Google Scholar
Heckmann, R. (1996). Spaces of valuations. In: Andima, S., Flagg, R. C., Itzkowitz, G., Misra, P., Kong, Y. and Kopperman, R. (eds.) Papers on General Topology and Applications: Eleventh Summer Conference at the University of Southern Maine, vol. 806. Annals of the New York Academy of Sciences, 174–200.CrossRefGoogle Scholar
Heckmann, R. and Keimel, K. (2013). Quasicontinuous domains and the Smyth powerdomain. In: Kozen, D. and Mislove, M. (eds.), Proceedings of the 29th Conference on the Mathematical Foundations of Programming Semantics, vol. 298. Electronic Notes in Theoretical Computer Science. Elsevier Science Publishers B.V., 215–232.CrossRefGoogle Scholar
Ho, W. K., Goubault-Larrecq, J., Jung, A. and Xi, X. (2018). The Ho-Zhao problem. Logical Methods in Computer Science 14 (1).Google Scholar
Isbell, J. (1982). Completion of a construction of Johnstone. Proceedings of the American Mathematical Society 85 333–334.CrossRefGoogle Scholar
Jia, X., Jung, A. and Li, Q. (2016). A note on coherence of dcpos. Topology and Its Applications 209 235–238.CrossRefGoogle Scholar
Jia, X., Lindenhovius, B., Mislove, M. and Zamdzhiev, V. (2021). Commutative monads for probabilistic programming languages. In: Logic in Computer Science (LICS 2021).Google Scholar
Jones, C. (1990). Probabilistic Non-Determinism. PhD thesis, University of Edinburgh, Edinburgh. Also published as Technical Report No. CST-63-90.Google Scholar
Jones, C. and Plotkin, G. (1989). A probabilistic powerdomain of evaluations. In: Proceedings of the 4th Annual Symposium on Logic in Computer Science. IEEE Computer Society Press, 186–195.CrossRefGoogle Scholar
Johnstone, P. T. (1981). Scott is not always sober. In: Continuous Lattices, Proceedings Bremen 871 282–283.CrossRefGoogle Scholar
Lyu, Z. and Jia, X. (July 2019). Core-compactness of smyth powerspaces. Available at https://arxiv.org/abs/1907.04715 Google Scholar
Royden, H. L. (1988). Real Analysis, 3rd edition. Macmillan.Google Scholar
Sorgenfrey, R. H. (1947). On the topological product of paracompact spaces. Bulletin of the American Mathematical Society 53 631–632.CrossRefGoogle Scholar
Tix, R. (June 1995). Stetige Bewertungen auf topologischen Räumen. Master’s thesis, Technische Hochschule Darmstadt, 51pp.Google Scholar
Xi, X. and Lawson, J. (2017). On well-filtered spaces and ordered sets. Topology and Its Applications 228 139–144.CrossRefGoogle Scholar
Xu, X. and Yang, Z. (2021). Coincidence of the upper vietoris topology and the scott topology. Topology and Its Applications 288 107480.CrossRefGoogle Scholar