Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T11:01:17.410Z Has data issue: false hasContentIssue false
  • English
  • Français

E-Unification based on Generalized Embedding

Published online by Cambridge University Press:  24 March 2022

Peter Szabo  and
Jörg Siekmann Open the ORCID record for Jörg Siekmann [Opens in a new window]
Peter Szabo
Affiliation:
Kurt-Schumacher-Str. 13, D-75180 Pforzheim, Germany
Jörg Siekmann*
Affiliation:
Saarland University/DFKI, Stuhlsatzenhausweg 3, D-66123 Saarbrücken, Germany
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Ordering is a well-established concept in mathematics and also plays an important role in many areas of computer science, where quasi-orderings, most notably well-founded quasi-orderings and well-quasi-orderings, are of particular interest. This paper deals with quasi-orderings on first-order terms and introduces a new notion of unification based on a special quasi-order, known as homeomorphic tree embedding. Historically, the development of unification theory began with the central notion of a most general unifier based on the subsumption order. A unifier 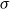$\sigma$ is most general, if it subsumes any other unifier $\tau$ , that is, if there is a substitution 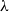$\lambda$ with 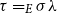$\tau=_{E}\sigma\lambda$ , where E is an equational theory and 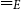$=_{E}$ denotes equality under E. Since there is in general more than one most general unifier for unification problems under equational theories E, called E-Unification, we have the notion of a complete and minimal set of unifiers under E for a unification problem 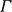$\varGamma$ , denoted as 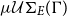$\mu\mathcal{U}\Sigma_{E}(\Gamma)$ . This set is still the basic notion in unification theory today. But, unfortunately, the subsumption quasi-order is not a well-founded quasi-order, which is the reason why for certain equational theories there are solvable E-unification problems, but the set $\mu\mathcal{U}\Sigma_{E}(\Gamma)$ does not exist. They are called type nullary in the unification hierarchy. In order to overcome this problem and also to substantially reduce the number of most general unifiers, we extended the well-known encompassment order on terms to an encompassment order on substitutions (modulo E). 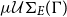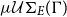Unification under the encompassment order is called essential unification and if $\mu\mathcal{U}\Sigma_{E}(\Gamma)$ exists, then the complete set of essential unifiers 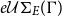$e\mathcal{U}\Sigma_{E}(\Gamma)$ is a subset of 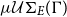$\mu\mathcal{U}\Sigma_{E}(\Gamma)$ . An interesting effect is that many E-unification problems with an infinite set of most general unifiers (under the subsumption order) reduce to a problem with only finitely many essential unifiers. Moreover, there are cases of an equational theory E, for which the complete set of most general unifiers does not exist, the minimal and complete set of essential unifiers however does exist. Unfortunately again, the encompassment order is not a well-founded quasi-ordering either, that is, there are still theories with a solvable unification problem, for which a minimal and complete set of essential unifiers does not exist. This paper deals with a third approach, namely the extension of the well-known homeomorphic embedding of terms to a homeomorphic embedding of substitutions (modulo E). We examine the set of most general, minimal, and complete E-unifiers under the quasi-order of homeomorphic embedment modulo an equational theory E, called 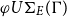$\varphi U\Sigma_{E}(\Gamma)$ , and propose an appropriate definitional framework based on the standard notions of unification theory extended by notions for the tree embedding theorem or Kruskal’s theorem as it is called. 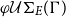The main results are that for regular theories the minimal and complete set $\varphi\mathcal{U}\Sigma_{E}(\Gamma)$ always exists. If we restrict the E-embedding order to pure E-embedding, a well-known technique in logic programming and term rewriting where the difference between variables is ignored, the set 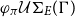$\varphi_{\pi}\mathcal{U}\Sigma_{E}(\Gamma)$ always exists and it is even finite for any theory E.

Keywords

Universal algebraequational theoryorderingunification theoryE-unificationessential unification(homeomorphic) embedded E-unifierspure E-unifiers
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Issue 8 , September 2021 , pp. 898 - 917
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alpuente, M., Cuenca-Ortega, A., Escobar, S. and Meseguer, J. (2016). Partial evaluation of order-sorted equational programs modulo axioms. In: Hermenegildo M. and Lopez-Garcia P. (eds.) Logic-Based Program Synthesis and Transformation, LOPSTR 2016. Lecture Notes in Computer Science, vol. 10184. Springer.Google Scholar
Alpuente, M., Cuenca-Ortega, A., Escobar, S. and Meseguer, J. (2018). Homeomorphic embedding modulo combinations of associativity and commutativity axioms. In: International Symposium on Logic-Based Program Synthesis and Transformation. Springer, pp. 38–55.Google Scholar
Baader, F. (1988). A note on unification type zero. Information Processing Letters 27 91–93.CrossRefGoogle Scholar
Baader, F. and Ghilardi, S. (2011). Unification in modal and description logics. Logic Journal of GPL 19 (6).Google Scholar
Baader, F. and Nipkow, T. (1998). Term Rewriting and all That. Cambridge University Press.CrossRefGoogle Scholar
Baader, F. and Siekmann, J. (1994). General unification theory. In: Gabbay, D., Hogger, C. and Robinson, J. (eds.) Handbook of Logic in Artificial Intelligence and Logic Programming. Oxford University Press, pp. 41–126.Google Scholar
Baader, F. and Snyder, W. (2001). Unification theory. In: Robinson, A. and Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. 1. Elsevier Science Publishers.Google Scholar
Cabrer, L. M. and Metcalfe, G. (2014). From admissibility to a new hierarchy of unification types. RISC 41,Linz.Google Scholar
Cabrer, L. M. and Metcalfe, G. (2015). Exact unification and admissibility. Logical Methods in Computer Science 11 (3).Google Scholar
Dershowitz, N. (1982). Orderings for term-rewriting systems. Theoretical Computer Science 17, 279–301.CrossRefGoogle Scholar
Dershowitz, N. (1987). Termination of rewriting. Journal of Symbolic Computation 3 (1) 69–115.CrossRefGoogle Scholar
Dershowitz, N. and Jouannaud, J.-P. (1990). Rewrite systems. In: van Leeuwen, J. (ed.), Handbook of Theoretical Computer Science. Elsevier Science Publishers (North-Holland),, pp. 244–320.CrossRefGoogle Scholar
Dershowitz, N. and Jouannaud, J.-P. (1991). Notations for rewriting. Bulletin of the EATCS 43, 162–174.Google Scholar
Gallier, J. H. (1991). Unification procedures in automated deduction methods based on matings: A survey. Technical Report CIS-436, University of Pennsylvania, Department of Computer and Information Science.Google Scholar
Gallier, J. H. (1991). What’s so special about Kruskal’s theorem and the ordinal gamma0 ?: A survey of some results in proof theory. Annals of Pure and Applied Logic 53 (3) 199–260.CrossRefGoogle Scholar
Ghilardi, S. (2018). Handling substitutions via duality. In: Proceedings of the International Workshop on Unification Theory (UNIF32), FLoC2018, Oxford.Google Scholar
Ghilardi, S. (1997). Unification through projectivity. Journal of Logic and Computation 7 (3).CrossRefGoogle Scholar
Higman, G. (1952). Ordering by divisibility in abstract algebras. Proceedings of the London Mathematical Society, 3 (1) 326–336.CrossRefGoogle Scholar
Hoche, M., Siekmann, J. and Szabo, P. (2008). String unification is essentially infinitary. In: Marin, M. (ed.) The 22nd International Workshop on Unification (UNIF 2008), Hagenberg, Austria, pp. 82–102.Google Scholar
Hoche, M., Siekmann, J. and Szabo, P. (2016). String unification is essentially infinitary. IFCoLog Journal of Logics and their Applications.Google Scholar
Hoche, M. and Szabo, P. (2006). Essential unifiers. Journal of Applied Logic 4 (1) 1–25.CrossRefGoogle Scholar
Knight, K. (1989). Unification: A multidisciplinary survey. ACM Computing Surveys (CSUR) 21 (1) 93–124.CrossRefGoogle Scholar
Kruskal, J. B. (1960). Well-quasi-ordering, the tree theorem and VÁzsonyi’s conjecture. Transactions of the American Mathematical Society 95 210–225.Google Scholar
Kruskal, J. B. (1972). The theory of well-quasi-ordering: A frequently discovered concept. Journal of Combinatorial Theory 13 297–305.CrossRefGoogle Scholar
Leuschel, M. (1998). Improving homeomorphic embedding for online termination. In: International Workshop on Logic Programming Synthesis and Transformation. Berlin, Heidelberg: Springer.Google Scholar
Leuschel, M. (2002). Homeomorphic embedding for online termination of symbolic methods. In: The Essence of Computation. Lecture Notes in Computer Science, vol. 2566. Berlin, Heidelberg: Springer.Google Scholar
Nash-Williams, C. St. J. A. (1963). On well-quasi-ordering finite trees. In: Green, B. J. (ed.) Mathematical Proceedings of the Cambridge Philosophical Society, vol. 59. 04. Cambridge Philosophical Society, pp. 833–835.Google Scholar
Robinson, J. A. (1965). A machine-oriented logic based on the resolution principle. Journal of the ACM 12 (1) 23–41.CrossRefGoogle Scholar
Siekmann, J. (1989). Unification theory. Journal of Symbolic Computation 7 (3 & 4) 207–274.CrossRefGoogle Scholar
Singh, D., Shuaibu, A. M. and Ndayawo, M. S. (2013). Simplified proof of Kruskals tree theorem. Mathematical Theory and Modeling 3 (13) 93–100.Google Scholar
Szabo, P., Siekmann, J. and Hoche, M. (2016). What is essential unification? In: Martin Davis on Computability, Computation, and Computational Logic. Springer’s Series “Outstanding Contributions to Logic”.Google Scholar
Szabo, P. and Siekmann, J. E-Unification based on Generalized Embedding. Mathematical Structures in Computer Science. https://doi.org/10.1017/S0960129522000019 Google Scholar