Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-18T04:47:43.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Computations with oracles that measure vanishing quantities

Published online by Cambridge University Press:  23 June 2016

EDWIN BEGGS ,
JOSÉ FÉLIX COSTA ,
DIOGO POÇAS  and
JOHN V. TUCKER
EDWIN BEGGS
Affiliation:
College of Science, Swansea University, Swansea, SA2 8PP, Wales, U.K. Emails: [email protected], [email protected]
JOSÉ FÉLIX COSTA
Affiliation:
Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal Email: [email protected]
DIOGO POÇAS
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, L8S 4K1, Canada Email: [email protected]
JOHN V. TUCKER
Affiliation:
College of Science, Swansea University, Swansea, SA2 8PP, Wales, U.K. Emails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider computation with real numbers that arise through a process of physical measurement. We have developed a theory in which physical experiments that measure quantities can be used as oracles to algorithms and we have begun to classify the computational power of various forms of experiment using non-uniform complexity classes. Earlier, in Beggs et al. (2014 Reviews of Symbolic Logic7(4) 618–646), we observed that measurement can be viewed as a process of comparing a rational number z – a test quantity – with a real number y – an unknown quantity; each oracle call performs such a comparison. Experiments can then be classified into three categories, that correspond with being able to return test results

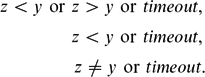$$\begin{eqnarray*} z < y\text{ or }z > y\text{ or }\textit{timeout},\\ z < y\text{ or }\textit{timeout},\\ z \neq y\text{ or }\textit{timeout}. \end{eqnarray*} $$
These categories are called two-sided, threshold and vanishing experiments, respectively. The iterative process of comparing generates a real number y. The computational power of two-sided and threshold experiments were analysed in several papers, including Beggs et al. (2008 Proceedings of the Royal Society, Series A (Mathematical, Physical and Engineering Sciences)464 (2098) 2777–2801), Beggs et al. (2009 Proceedings of the Royal Society, Series A (Mathematical, Physical and Engineering Sciences)465 (2105) 1453–1465), Beggs et al. (2013a Unconventional Computation and Natural Computation (UCNC 2013), Springer-Verlag 6–18), Beggs et al. (2010b Mathematical Structures in Computer Science20 (06) 1019–1050) and Beggs et al. (2014 Reviews of Symbolic Logic, 7 (4):618-646). In this paper, we attack the subtle problem of measuring physical quantities that vanish in some experimental conditions (e.g., Brewster's angle in optics). We analyse in detail a simple generic vanishing experiment for measuring mass and develop general techniques based on parallel experiments, statistical analysis and timing notions that enable us to prove lower and upper bounds for its computational power in different variants. We end with a comparison of various results for all three forms of experiments and a suitable postulate for computation involving analogue inputs that breaks the Church–Turing barrier.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Special Issue 8: Continuity, Computability, Constructivity: From Logic to Algorithms 2013 , December 2017 , pp. 1315 - 1363
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balcázar, J.L., Días, J. and Gabarró, J. (1990). Structural Complexity I, 2nd edition, Springer-Verlag.Google Scholar
Beggs, E., Costa, J.F., Loff, B. and Tucker, J.V. (2008). Computational complexity with experiments as oracles. Proceedings of the Royal Society, Series A (Mathematical, Physical and Engineering Sciences) 464 (2098) 2777–2801.Google Scholar
Beggs, E., Costa, J.C., Loff, B. and Tucker, J.V. (2009). Computational complexity with experiments as oracles II. Upper bounds. Proceedings of the Royal Society, Series A (Mathematical, Physical and Engineering Sciences) 465 (2105) 1453–1465.Google Scholar
Beggs, E., Costa, J.F., Poças, D. and Tucker, J.V. (2013a). On the power of threshold measurements as oracles. In: Mauri, G., Dennunzio, A., Manzoni, L. and Porreca, A.E. (eds.) Unconventional Computation and Natural Computation (UCNC 2013), Lecture Notes in Computer Science, volume 7956, Springer-Verlag, 6–18.Google Scholar
Beggs, E., Costa, J.F., Poças, D. and Tucker, J.V. (2013b). Oracles that measure thresholds: The turing machine and the broken balance. Journal of Logic and Computation 23 (6) 1155–1181.CrossRefGoogle Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2010a). Computational models of measurement and Hempel's axiomatization. In: Carsetti, A. (ed.) Causality, Meaningful Complexity and Knowledge Construction, Theory and Decision Library A, volume 46, Springer-Verlag, 155–184.Google Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2010b). Limits to measurement in experiments governed by algorithms. Mathematical Structures in Computer Science 20 (06) 1019–1050. Special issue on Quantum Algorithms, editor Salvador Elías Venegas-Andraca.Google Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2010c). Physical oracles: The Turing machine and the Wheatstone bridge. Studia Logica 95 (1–2) 279–300. Special issue on Contributions of Logic to the Foundations of Physics, editors D. Aerts, S. Smets & J. P. Van Bendegem.Google Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2010d). The Turing machine and the uncertainty in the measurement process. In: Guerra, H. (ed.) Physics and Computation, P&C 2010, CMATI – Centre for Applied Mathematics and Information Technology, University of Azores, 62–72.Google Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2012a). Axiomatising physical experiments as oracles to algorithms. Philosophical Transactions of the Royal Society, Series A (Mathematical, Physical and Engineering Sciences) 370 (12) 3359–3384.Google Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2012b). The impact of models of a physical oracle on computational power. Mathematical Structures in Computer Science 22 (5) 853–879. Special issue on Computability of the Physical, editors Cristian S. Calude and S. Barry Cooper.Google Scholar
Beggs, E., Costa, J.F. and Tucker, J.V. (2014). Three forms of physical measurement and their computability. Reviews of Symbolic Logic 7 (4) 618–646.Google Scholar
Beggs, E. and Tucker, J.V. (2006). Embedding infinitely parallel computation in Newtonian kinematics. Applied Mathematics and Computation 178 (1) 25–43.Google Scholar
Beggs, E. and Tucker, J.V. (2007a). Can Newtonian systems, bounded in space, time, mass and energy compute all functions? Theoretical Computer Science 371 (1) 4–19.Google Scholar
Beggs, E. and Tucker, J.V. (2007b). Experimental computation of real numbers by Newtonian machines. Proceedings of the Royal Society, Series A (Mathematical, Physical and Engineering Sciences) 463 (2082) 1541–1561.Google Scholar
Bekey, G.A. and Karplus, W.J. (1968). Hybrid Computation, John Wiley & Sons.Google Scholar
Born, M. and Wolf, E. (1964). Principles of Optics. Electromagnetic Theory of Propagation, Interference and Diffraction of Light, second (revised) edition, Pergamon Press.Google Scholar
Bournez, O. and Cosnard, M. (1996). On the computational power of dynamical systems and hybrid systems. Theoretical Computer Science 168 (2) 417–459.CrossRefGoogle Scholar
Carnap, R. (1966). Philosophical Foundations of Physics, Basic Books.Google Scholar
Geroch, R. and Hartle, J.B. (1986). Computability and physical theories. Foundations of Physics 16 (6) 533–550.Google Scholar
Hempel, C.G. (1952). Fundamentals of concept formation in empirical science. International Encyclopedia of Unified Science, volume 2 no. 7, Chicago Univ. Press.Google Scholar
Krantz, D.H., Suppes, P., DuncanAAAALuce, R. and Tversky, A. (1990). Foundations of Measurement, vol. 1 (1971), vol. 2 (1989) and vol. 3 (1990), Academic Press.Google Scholar
Kreisel, G. (1974). A notion of mechanistic theory. Synthese 29 (1) 11–26.Google Scholar
Pauly, A. (2009). Representing measurement results. Journal of Universal Computer Science 15 (6) 1280–1300.Google Scholar
Pauly, A. and Ziegler, M. (2013). Relative computability and uniform continuity of relations. Journal of Logic and Analysis 5 (7) 139.Google Scholar
Pour-El, M. (1974). Abstract computability and its relations to the general purpose analog computer. Transactions of the American Mathematical Society 199 1–28.Google Scholar
Pour-El, M. and Richards, I. (1979). A computable ordinary differential equation which possesses no computable solution. Annals of Mathematical Logic 17 (1–2) 61–90.Google Scholar
Pour-El, M. and Richards, I. (1981). The wave equation with computable initial data such that its unique solution is not computable. Advances in Mathematics 39 (4) 215–239.Google Scholar
Pour-El, M. and Richards, I. (1989). Computability in Analysis and Physics, Perspectives in Mathematical Logic, Springer-Verlag.Google Scholar
Siegelmann, H.T. and Sontag, E.D. (1994). Analog computation via neural networks. Theoretical Computer Science 131 (2) 331–360.Google Scholar
Weihrauch, K. (2000). Computable Analysis, Springer-Verlag.CrossRefGoogle Scholar
Weihrauch, K. and Zhong, N. (2002). Is wave propagation computable or can wave computers beat the Turing machine? Proceedings of the London Mathematical Society 85 (2) 312–332.Google Scholar
Woods, D. and Naughton, T.J. (2005). An optical model of computation. Theoretical Computer Science 334 (1–3) 227–258.Google Scholar
Ziegler, M. (2009). Physically-relativized Church-Turing hypotheses: Physical foundations of computing and complexity theory of computational physics. Applied Mathematics and Computation 215 (4) 1431–1447.Google Scholar