Article contents
An improved primal-dual approximation algorithm for the k-means problem with penalties
Published online by Cambridge University Press: 16 August 2021
Abstract
In the k-means problem with penalties, we are given a data set 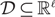 $${\cal D} \subseteq \mathbb{R}^\ell $$ of n points where each point
$${\cal D} \subseteq \mathbb{R}^\ell $$ of n points where each point 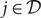 $$j \in {\cal D}$$ is associated with a penalty cost pj and an integer k. The goal is to choose a set
$$j \in {\cal D}$$ is associated with a penalty cost pj and an integer k. The goal is to choose a set 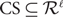 $${\rm{C}}S \subseteq {{\cal R}^\ell }$$ with |CS| ≤ k and a penalized subset
$${\rm{C}}S \subseteq {{\cal R}^\ell }$$ with |CS| ≤ k and a penalized subset 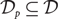 $${{\cal D}_p} \subseteq {\cal D}$$ to minimize the sum of the total squared distance from the points in D / Dp to CS and the total penalty cost of points in Dp, namely
$${{\cal D}_p} \subseteq {\cal D}$$ to minimize the sum of the total squared distance from the points in D / Dp to CS and the total penalty cost of points in Dp, namely 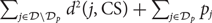 $$\sum\nolimits_{j \in {\cal D}\backslash {{\cal D}_p}} {d^2}(j,{\rm{C}}S) + \sum\nolimits_{j \in {{\cal D}_p}} {p_j}$$. We employ the primal-dual technique to give a pseudo-polynomial time algorithm with an approximation ratio of (6.357+ε) for the k-means problem with penalties, improving the previous best approximation ratio 19.849+∊ for this problem given by Feng et al. in Proceedings of FAW (2019).
$$\sum\nolimits_{j \in {\cal D}\backslash {{\cal D}_p}} {d^2}(j,{\rm{C}}S) + \sum\nolimits_{j \in {{\cal D}_p}} {p_j}$$. We employ the primal-dual technique to give a pseudo-polynomial time algorithm with an approximation ratio of (6.357+ε) for the k-means problem with penalties, improving the previous best approximation ratio 19.849+∊ for this problem given by Feng et al. in Proceedings of FAW (2019).
- Type
- Special Issue: Theory and Applications of Models of Computation (TAMC 2020)
- Information
- Mathematical Structures in Computer Science , Volume 32 , Issue 2: Theory and Applications of Models of Computation (TAMC 2020) , February 2022 , pp. 151 - 163
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
†A preliminary version of this paper appeared in Proceedings of the 16th Annual Conference on Theory and Applications of Models of Computation, pp. 377–389, 2020
References
- 1
- Cited by



