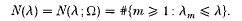Research Article
Discrete coactions on Hilbert C*-modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-112
-
- Article
- Export citation
On Hausdorff and packing dimension of product spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 715-727
-
- Article
- Export citation
On the almost sure approximation of self-adjoint operators in L2 (0, 1)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 537-543
-
- Article
- Export citation
Compactifications and A-compactifications of frames. Proximal frames
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-339
-
- Article
- Export citation
Beurling's projection theorem via one-dimensional Brownian motion
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 729-738
-
- Article
- Export citation
Examples of tunnel number one knots which have the property ‘1 + 1 = 3’
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-118
-
- Article
- Export citation
Differential invariants of ℝ*-structures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-356
-
- Article
- Export citation
On the contractibility to a point of the linear groups of reflexive non-commutative Lp-spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-560
-
- Article
- Export citation
On the zeros and Fourier transforms of entire functions in the Paley–Wiener space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-362
-
- Article
- Export citation
Cosmological solutions of the Vlasov-Einstein system with spherical, plane, and hyperbolic symmetry
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 739-762
-
- Article
- Export citation
Sublinear discrete-time order-preserving dynamical systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 561-574
-
- Article
- Export citation
Unstable homotopy classification of
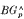
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-137
-
- Article
- Export citation
Front matter
PSP volume 119 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Normal solutions of elliptic equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-371
-
- Article
- Export citation
Glueing operation for R-matrices, quantum groups and link-invariants of Hecke type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-166
-
- Article
- Export citation
Front matter
PSP volume 119 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Geometric characterization of linearisable second-order differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-381
-
- Article
- Export citation
Back matter
PSP volume 119 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Counterexamples to the modified Weyl–Berry conjecture on fractal drums
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-178
-
- Article
- Export citation
Back matter
PSP volume 119 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b7
-
- Article
-
- You have access
- Export citation


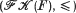 of all (up to equivalence) regular compactifications of a completely regular frame.
of all (up to equivalence) regular compactifications of a completely regular frame.  isomorphic to the category
isomorphic to the category  of
of 

 is order-preserving and sublinear. If every positive semi-orbit has compact closure, then every positive semi-orbit converges to a fixed point. This result does not require that the order be strongly preserved.
is order-preserving and sublinear. If every positive semi-orbit has compact closure, then every positive semi-orbit converges to a fixed point. This result does not require that the order be strongly preserved.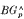
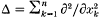 be the Laplacian operator. Consider the eigenvalue problem (with Dirichlet boundary conditions):
be the Laplacian operator. Consider the eigenvalue problem (with Dirichlet boundary conditions):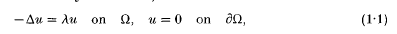
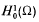 (the closure in the Sobolev space
(the closure in the Sobolev space 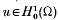 are positive and form a discrete set. Moreover, for each λ, the associated eigenspace is finite dimensional. Let the spectrum of (1·1) be denoted
are positive and form a discrete set. Moreover, for each λ, the associated eigenspace is finite dimensional. Let the spectrum of (1·1) be denoted 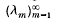 where 0 < λ
where 0 < λ