We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is indicated by means of a particular example how an inconsistency arises in one formulation of diffraction problems. It is shown that the inconsistency is removed if different boundary conditions are imposed during the formulation. In the proof it is necessary to determine the contributions to the field from parts of a sphere of radius R at an interior point when the field on the sphere is a plane wave. It is found that, as R → ∞, the part of the sphere near the source which subtends a solid angle of order 
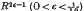at the centre contributes the plane wave and that the remainder of the sphere provides a contribution which vanishes in the limit. The demonstration involves the use of the principle of stationary phase for an integral of two variables.
In the final section special boundary conditions are given for an exceptional three-dimensional problem.