We often wish to test the difference of the means of two series of measures of a quantity for a systematic difference. A suitable test, in terms of the theory of probability, can be obtained as follows. We suppose that in each series the probability of error is normally distributed with unknown standard error. Then if we have only one observation in each series, the difference of the two could equally well be interpreted as entirely due to the random error in one series, the other being right, or entirely due to systematic difference, both observations being free from random error. This suggests that we should take as one of our fundamental quantities the expectation of the difference of a single measure in one series from one in the other; the expectation of the square of the difference, however, appears still better.

1. Introduction and summary. The problem of the elastic stability of a simply supported rectangular plate, compressed by two equal and opposite forces acting in the plane of the plate (see Fig. 1), was first attempted by A. Sommerfeld, and later by S. Timoshenko. The former produced a solution which in a later paper he admitted to be liable to very considerable error, while the latter constructed a solution by means of the well-known strain-energy method. In many problems this method gives results in very close agreement with those obtained in a more rigorous manner, but, in the particular case considered here, it appeared likely that the error would be appreciable owing to the underlying assumption that the only stresses in the plate occurred along the common line of action of the two external forces.

A definition of “closer” and “closest” as applied to estimates of statistical parameters is given, and it is shown that we can sometimes prove that estimates properly derived from sufficient statistics are the closest possible.

The scaling of a gamma distribution, and the location and scaling of an exponential distribution and of a rectangular distribution are discussed in detail, and the closest estimates of the parameters obtained.

1. A well-known theorem on probability may be stated as follows. Let λdt be the chance that a certain event will happen in time dt, so that λT is the average number of occurrences of the event in an interval T. If we take a large number of repetitions of the interval T the actual numbers of occurrences will fluctuate about the mean λT, being say λT + x′, λT + x″,…. Then the theorem states that

The ejection of an α-particle by a radioactive substance is an event of the type contemplated and the theorem was applied to this physical problem by von Schweidler in 1905. Much similar work, both theoretical and experimental, has been done at intervals since then*.

In an excursus developing a modern view of the Carnot-Kelvin aspect of thermodynamics, appended recently to the letters from Clerk Maxwell to his friend W. Thomson reporting the early tentative evolution of the theory of the electro-dynamic field, the account presented by the writer stopped short at putting emphasis on the mystery of temperature, as a unique and supremely significant property of matter in bulk, with its trend to uniformity as presenting the basic thermal problem. The side of the subject involving dynamical analogy was there absent from the development, which was purely formal. It may be well, however, now to offer some general notions such as may be put on record, which arise naturally from that mode of approach to the subject.

The differential analyser has been used to evaluate solutions of the equation

with boundary conditions y = y′ = 0 at x = 0, y′ → 1 as x → ∞, which occurs in Falkner and Skan's approximate treatment of the laminar boundary layer. A numerical iterative method has been used to improve the accuracy of the solutions, and the results show that the accuracy of the machine solutions is about 1 in 1000, or rather better.

It is shown that the conditions are insufficient to specify a unique solution for negative values of β a discussion of this situation is given, and it is shown that for the application to be made of the solution the appropriate condition is that y′ → 1 from below, and as rapidly as possible, as x → ∞. The condition that y′ → 1 from below can be satisfied only for values of β0, greater than a limiting value β0, whose value is approximately − 0·199, and which is related to the point at which the laminar boundary layer breaks away from the boundary.

1. The elastic stability of a long flat plate when acted on by a shearing force along its edges has been discussed by Southwell and Skan*, and Leggett† has solved the shearing problem when the plate has a small constant curvature. The present paper deals with the elastic stability of a long corrugated plate which is acted on by a shearing force along its generators, the work being applicable to plates with any given number of bays forming the corrugations. It is supposed that the plate is thin and that the depth d of a bay is a small multiple of the semithickness h; little progress has been made without some such assumption as the second, which enables us to reduce the fundamental equations to a soluble form.

The stability of the motion of viscous incompressible fluid, of density ρ and kinematic viscosity ν, between two infinitely long coaxial circular cylinders, of radii a and a + d, where d/a is small, is investigated mathematically by the method of small oscillations. The inner cylinder is rotating with angular velocity ω and the outer one with angular velocity αω, and there is a constant pressure gradient parallel to the axis. The fluid therefore has a component velocity W parallel to the axis, in addition to the velocity round the axis. A disturbance is assumed which is symmetrical about the axis and periodic along it. The critical disturbance, which neither increases nor decreases with the time, is periodic with respect to the time (except when W = 0, when the critical disturbance is a steady motion). As Reynolds number of the flow we take | 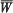| d/ν, where 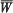is the average value of W across the annulus, and we denote by l the wave-length of the disturbance along the axis, by σ/2π the time period of the critical flow, by c the wavelength of the critical flow, by ωc the critical value of ω, and we put

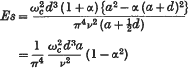
approximately, if α is not nearly equal to 1.

The previous paper dealt first with the shot effect without secondary emission. We considered a stream of electrons arriving at random, with a fixed probable density N, at the anode of the resistance-capacity coupled first valve of a linear amplifier. This does not allow for the effect whereby the arrival of electrons alters the anode potential, and consequently the probability of arrival of succeeding electrons. The valve must be working with what is conventionally called an infinite internal resistance, and without space-charge effects. Each electron arriving at time tr is supposed to produce at time t an output effect f(t − tr) from the amplifier. We considered the hypotheses, first, that electrons may, with specific probabilities, have lives of any length on the anode system, during which they add − ε/C to the anode potential, and alternatively that each electron adds to the anode potential of the valve whose anode to earth capacity is C and whose feed resistance is R. These hypotheses determine the form of f(t − tr) when the behaviour of the main part of the amplifier is known. Since the amplifier is linear, the effects of various electrons are additive, so that the total output is ∂(t) = ∑rf(t − tr).

The solution of problems in two-dimensional potential theory depends, generally speaking, on the discovery of a conformal transformation suitable for the particular region involved, and the degree of success in the applicability of the method seems to be seriously limited by the complexity of the transformation. Only one serious attempt seems to have been made, by W. G. Bickley*, to formulate a general theory coordinating the different types of boundary value problem for general and inclusive classes of curves, but Bickley's analysis is somewhat involved and not very suitable for certain types of problem. In a re-examination of the subject on the basis of certain suggestions made to me by Prof. Livens, I have discovered what appears to be a much simpler and equally general method of formulating directly the solution for a comprehensive class of problem dealing with simple closed cylinders with curved or rectilinear boundaries, and including all those cases for which solutions are known. In its theoretical aspects the method seems to be perfectly general, but to put it into practice it is necessary to determine explicitly the particular form for the conformal transformation of the space outside the cross-section of the cylinder to the space outside a circle with the points at infinity coinciding.

The following theoretical investigation of the two-dimensional flow of an inviscid fluid past a keel and rudder, and of the consequent lateral force, follows experiments performed by Prof. T. B. Abell in the Department of Naval Architecture of the University of Liverpool, and we wish to acknowledge our indebtedness to him for the information given in many discussions.

The ratios of the inter-multiplet separations for the lowest states of O, O+ and O++ obtained by Slater's method depart considerably from the observed values. In this method it is assumed that matrix elements of the Hamiltonian involving two different configurations are negligible, so that each state can be described by a single configuration, whereas these matrix elements are probably appreciable, and a better approximation is obtained by use of a wave function corresponding to a superposition of more than one configuration. The effect of this superposition of configurations has been called “configuration interaction”, and the general theory of it is discussed in Condon and Shortley's Theory of atomic spectra, Chap. xv. It is shown that it occurs only between terms of the same L and S, and of the same parity (∑l even or odd). Few quantitative applications, however, have yet been made. A calculation by Bacher for Mg shows that the effect can be considerable although the states are quite widely separated.

1. Introduction. The importance of the frequency spectrum of the lattice in problems concerning the properties of the crystalline state has often been emphasized. In particular, all the properties of a crystal which depend on the heat motion of the constituent particles require for their explanation a knowledge of the actual form of the vibrational spectrum.

A method of obtaining an approximate solution of Schrödinger's equation with a non-central field of force is given for the case when a solution of a similar equation involving the angular coordinates only is known.

In conclusion I should like to thank Prof. J. E. Lennard-Jones, F.R.S., for suggesting the problem and for his continued interest in it, and also the Department of Scientific and Industrial Research for a grant.

The type of integral considered, is of frequent occurrence in problems in the kinetic theory of gases and in particular is required in the paper which follows, in calculating viscosity. The result is an extension of one given by Berger, and the analysis follows closely the discussion of Gauss's formula for approximate quadrature in Whittaker and Robinson, The calculus of observations; the novelty lies in the use of Sonine polynomials, which are peculiarly well suited for the discussion of this type of integral.

There exists a group of action functions, depending on a parameter γ giving for every γ ≥ 0 a static solution with central symmetry and finite energy, both for the electric and magnetic field, and going over into Maxwell's action function for weak fields. For γ = 1 we obtain Born's case distinguished by a perfect symmetry between electric and magnetic field. For γ = 0 the action function takes a particularly simple form and the comparison with the results of Heisenberg, Euler and Kockel allows of an approximate determination of the fine structure constant.

A method of determining the coefficient of viscosity of a gas of spherically symmetrical molecules under ordinary conditions has been given by Chapman. His result is equivalent to

where m is the mass of a molecule of the gas, T is the absolute temperature, k is Boltzmann's constant 1·372. 10−16 and ε is a small quantity which later investigations on a gas in which the intermolecular force is inversely proportional to the nth power of the distance have shown to vary from zero when n = 5 to 0·016 when n = ∞ (equivalent to molecules which are elastic spheres); it may reasonably be supposed that ε is positive and less than 0·016 in all cases which are likely to be of interest, and it will be neglected in this paper. Also

π(r) being the mutual potential energy of two molecules (that is, the repulsive force between them is − ∂π/∂r), and r0 the positive zero of the expression in the denominator, or the largest such positive zero if there are several.

The statistical treatment of order-disorder transformations, as developed by Bethe and Peierls, has been extended to alloys having superlattices of the AB and AB3 types but compositions which differ slightly from the ideal compositions required for the formation of perfect superlattices. If the composition of the alloy is specified by the concentration c of one component, which we have chosen to be the A component, then the results show that for alloys of the AB type the critical temperature should have a maximum value when c = ½, that is, for the ideal composition. This is in agreement with experiment. For alloys of the AB3 type it is found that the maximum value should occur for some value of c > ¼. This result disagrees with that obtained experimentally, but both results agree, at least qualitatively, with those obtained by the theory of Bragg and Williams.

The object of this paper is to compare some of the wave functions which have been suggested for the normal helium atom, including one calculated in the first section of the paper, as regards energy, magnetic susceptibility and electric polarizability. Since this atom provides the simplest two-electron problem, such a comparison is of special interest and may indicate the direction in which improvements might be made in the calculation of wave functions for more complicated atoms.

Born's electrodynamics, together with its quantization, has been developed in several papers by Born and Infeld†. It is a general concept, containing many different systems of electrodynamics, of which Maxwell's theory is one particular case. Each system is characterized by a Lagrangian (or Hamiltonian) function of two invariants F and G (or P and Q). These invariants are built up by means of two antisymmetrical tensors, which are the “field quantities”.