The determination of intermolecular forces in gases from their viscosity
Published online by Cambridge University Press: 24 October 2008
Extract
A method of determining the coefficient of viscosity of a gas of spherically symmetrical molecules under ordinary conditions has been given by Chapman. His result is equivalent to
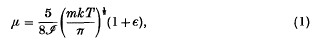
where m is the mass of a molecule of the gas, T is the absolute temperature, k is Boltzmann's constant 1·372. 10−16 and ε is a small quantity which later investigations on a gas in which the intermolecular force is inversely proportional to the nth power of the distance have shown to vary from zero when n = 5 to 0·016 when n = ∞ (equivalent to molecules which are elastic spheres); it may reasonably be supposed that ε is positive and less than 0·016 in all cases which are likely to be of interest, and it will be neglected in this paper. Also
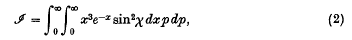
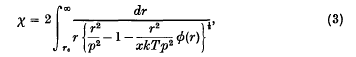
π(r) being the mutual potential energy of two molecules (that is, the repulsive force between them is − ∂π/∂r), and r0 the positive zero of the expression in the denominator, or the largest such positive zero if there are several.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 33 , Issue 3 , July 1937 , pp. 363 - 370
- Copyright
- Copyright © Cambridge Philosophical Society 1937
References
* Phil. Trans. Roy. Soc. 211 (1911), 433.Google Scholar
† Chapman, , Phil. Trans. Roy. Soc. 216 (1916), 279;CrossRefGoogle Scholar Enakog, Inaug. Diss. Upsala (1917); Burnett, , Proc. Lond. Math. Soc. (2) 39 (1935), 385.CrossRefGoogle Scholar
* For cases 1, 2, 3 see Chapman, loc. cit. (1916); for case 4 see Jones, , Proc. Roy. Soc. 106 (1924), 441.CrossRefGoogle Scholar
* Chapman, loc. cit. (1916), p. 338.
* In practice it is found that better approximations are obtained if y −2 increases by 2−3% more than ![]() when the temperature is doubled (from 225° to 450° K.).
when the temperature is doubled (from 225° to 450° K.).
* Landolt-Börnstein, , Physikalisch-Chemische Tabellen, 5th ed. (Berlin, 1923).Google Scholar
† Cf. Lennard-Jones, , Proc. Phys. Soc. 43 (1931), 461.CrossRefGoogle Scholar
- 6
- Cited by


