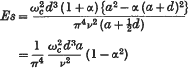Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Green, A. E.
1944.
Double Fourier series and boundary value problems.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 40,
Issue. 3,
p.
222.
1955.
On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk.
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences,
Vol. 248,
Issue. 943,
p.
155.
Budiansky, Bernard
and
Diprima, R. C.
1960.
Bending Vibrations of Uniform Twisted Beams.
Journal of Mathematics and Physics,
Vol. 39,
Issue. 1-4,
p.
237.
1962.
Experiments on the stability of spiral flow at low axial Reynolds numbers.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
Vol. 265,
Issue. 1321,
p.
198.
Nield, D. A.
1964.
Surface tension and buoyancy effects in cellular convection.
Journal of Fluid Mechanics,
Vol. 19,
Issue. 3,
p.
341.
Krueger, E. R.
and
Prima, R. C. Di
1964.
The stability of a viscous fluid between rotating cylinders with an axial flow.
Journal of Fluid Mechanics,
Vol. 19,
Issue. 4,
p.
528.
Datta, Subhendu K.
1965.
Stability of spiral flow between concentric circular cylinders at low axial Reynolds number.
Journal of Fluid Mechanics,
Vol. 21,
Issue. 4,
p.
635.
1968.
The developing tangential velocity profile for axial flow in an annulus with a rotating inner cylinder.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
Vol. 307,
Issue. 1488,
p.
55.
BALMER, ROBERT THEODORE
1970.
The Hygrocyst–a Stability Phenomenon in Continuum Mechanics.
Nature,
Vol. 227,
Issue. 5258,
p.
600.
Elliott, L.
1973.
Stability of a viscous fluid between rotating cylinders with axial flow and pressure gradient round the cylinders.
The Physics of Fluids,
Vol. 16,
Issue. 5,
p.
577.
Urintsev, A. L.
1977.
Calculation of the self-oscillations arising as a result of the loss of stability by the spiral flow of a viscous liquid in an annular tube.
Journal of Applied Mechanics and Technical Physics,
Vol. 17,
Issue. 3,
p.
344.
1979.
The stability of viscous flow between rotating concentric cylinders with an axial flow.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 366,
Issue. 1727,
p.
555.
Gabe, D. R.
and
Walsh, F. C.
1983.
The rotating cylinder electrode: a review of development.
Journal of Applied Electrochemistry,
Vol. 13,
Issue. 1,
p.
3.
Vidaurri, F. C.
and
Sherk, F. T.
1985.
Low backmixing in multistage agitated contactors used as reactors.
AIChE Journal,
Vol. 31,
Issue. 5,
p.
705.
Bühler, Karl
and
Polifke, Norbert
1990.
Nonlinear Evolution of Spatio-Temporal Structures in Dissipative Continuous Systems.
Vol. 225,
Issue. ,
p.
21.
Recktenwald, A.
Lücke, M.
and
Müller, H. W.
1993.
Taylor vortex formation in axial through-flow: Linear and weakly nonlinear analysis.
Physical Review E,
Vol. 48,
Issue. 6,
p.
4444.
Haim, D.
and
Pismen, L.M.
1994.
Performance of a photochemical reactor in the regime of Taylor-Görtler vortical flow.
Chemical Engineering Science,
Vol. 49,
Issue. 8,
p.
1119.
Büchel, P.
Lücke, M.
Roth, D.
and
Schmitz, R.
1996.
Pattern selection in the absolutely unstable regime as a nonlinear eigenvalue problem: Taylor vortices in axial flow.
Physical Review E,
Vol. 53,
Issue. 5,
p.
4764.
Cotrell, David L.
and
McFadden, G. B.
2005.
Linear stability of spiral Poiseuille flow with a radial temperature gradient: Centrifugal buoyancy effects.
Physics of Fluids,
Vol. 17,
Issue. 11,
Cotrell, David L.
and
McFadden, G. B.
2006.
Axial flow effects on the stability of circular Couette flow with viscous heating.
Physics of Fluids,
Vol. 18,
Issue. 8,
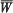 | d/ν, where
| d/ν, where 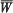 is the average value of W across the annulus, and we denote by l the wave-length of the disturbance along the axis, by σ/2π the time period of the critical flow, by c the wavelength of the critical flow, by ωc the critical value of ω, and we put
is the average value of W across the annulus, and we denote by l the wave-length of the disturbance along the axis, by σ/2π the time period of the critical flow, by c the wavelength of the critical flow, by ωc the critical value of ω, and we put