The free product A* B of groups A and B can be described in two ways.

We can construct the set of reduced words in A and B. Define a binary operation on by concatenating two words and performing as many reductions as possible. Prove that is a group; the difficult step is the proof of associativity. Define A * B = .

Introduction. Hall ((3), (4)) introduced the concept of a Sylow system and its normalizer into the theory of finite soluble groups. In (4) he showed that system normalizers may be characterized as those subgroups D of G minimal subject to the existence of a chain of subgroups from D up to G in which each subgroup is maximal and non-normal in the next; he also showed that a system normalizer covers all the central chief factors and avoids all the eccentric chief factors of G (for definitions of covering and avoidance, and an account of their elementary properties), the reader is referred to Taunt ((5)). This note arises out of an investigation into the question to what extent this covering/ avoidance property characterizes system normalizers; it provides a partial answer by means of two elementary counter-examples given in section 3 which seem to indicate that the property ceases to characterize system normalizers as soon as the ‘non-commutativity’ of the group is increased beyond a certain threshold. For the sake of completeness we include proofs in Theorems 1 and 2 of generalizations of two known results communicated to me by Dr Taunt and which as far as we know have not been published elsewhere. Theorem 1 shows the covering/avoidance property to be characteristic for the class of soluble groups with self-normalizing system normalizers introduced by Carter in (1), while Theorem 2 shows the same is true for A -groups (soluble groups with Abelian Sylow subgroups investigated by Taunt in (5)).

The examples are unconnected.

According to some published footnotes, examples are known of Serre fibrations which are not Hurewicz fibrations. However, as far as I know no such example has been published. The following example, which was stimulated by a more complicated example of G. Horrocks, seems worth mentioning, since it is extremely simple and does suggest some further questions.

If R is any ring then the set of isomorphism types of finitely generated projective right R-modules may be made into a semigroup by defining

.

Let Λ be the group of all real non-singular 2 × 2 matrices and let Ω be the group of all real 2 × 2 matrices with determinant 1 in which a matrix is identified with its negative. Then Ω is isomorphic to the group of all real linear fractional transformations of determinant 1. In a previous paper ((3)) the authors determined all faithful representations of the modular group (more generally of the Hecke groups) by a discrete subgroup of Ω, in which the representations were partitioned into conjugacy classes over Λ. In this paper we consider the question for the more general situation of the free product of any two cyclic groups of finite order. Our results parallel the results of (3) quite closely, but some significant differences in the details of the proofs arise. In particular Theorem 3 of section 3 below, which is purely group-theoretic, is of independent interest and should prove useful in other investigations.

Introduction. In this note we obtain a description of the structure of the minimal verbal subgroups of a finite group which has, among others, the following consequences:

Theorem 1. A finite group which belongs to the variety generated by its proper subgroups and proper factor-groups belongs either to the variety generated by its proper subgroups or to the variety generated by its proper factor-groups.

In an earlier paper (3), a non-abelian cohomology theory (in the dimensions 0 and 1) for associative algebras was developed. One of the objectives was to obtain equivalence classes of crossed homomorphisms by considering inner automorphisms of the coefficient-algebra. This paper is an adaptation of the methods employed there to the case of Lie algebras. Throughout, all our Lie algebras will be over the field of real numbers, and finite-dimensional.

If one of the locally compact groups H and K is of type I, the reduced dual of their product is shown to be homeomorphic to the product of the reduced duals.

In this paper we discuss the structure of a partially ordered set X by studying in detail certain subsets of X.

Let Q be the field of rational numbers, and let A be an Abelian curve (an Abelian variety of dimension one) defined over Q. Following Weil, the conductor of A is

where p runs over all primes, and the exponent is explained below; the primes dividing N are exactly those for which A has degenerate reduction modulo p.

Introductory. In the following pages a miscellany of information about M12, the Mathieu group of degree 12, is presented, mainly concerning its subgroups. The development is inspired by the work of Coxeter and Todd on the representation of M12 as a group of collineations in PG (5,3)—i.e. five-dimensional projective space over the field of 3 elements.

The abstract group

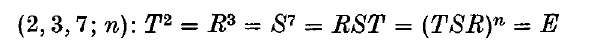
is finite for n = 4,6,7,8, and the relations are incompatible for n = 1,2,3,5. A criterion of Coxeter ((1)) suggests that (2,3,7; n) should be infinite for all n ≥ 9, but its applicability to these groups is unproved, and it is not known whether there are any further examples of finite groups (2,3,7; n). However, (2,3,7; 9) has been proved infinite by Sims ((3)), and it follows at once that (2,3,7; n) is infinite whenever n is a multiple of 9 as it then has an infinite factor group.

Conrad ((2)), has shown that any lattice group which obeys (C.F.) each strictly positive element exceeds at most a finite number of pairwise orthogonal elements may be constructed, from a family of simply ordered groups, by carrying out, alternately, the operations of forming finite direct sums and lexico extensions, at most a countable number of times. The main result of this paper, Theorem 3.1, gives necessary and sufficient conditions for a multilattice group, which obeys (ℋ*), to be isomorphic to a multilattice group which is constructed from a family of almost ordered groups, by carrying out, alternately, the operations of forming arbitrary direct sums and lexico extensions, any number of times; we call such a group a lexico sum of the almost ordered groups.

Introduction. In (1–3,6) it is shown that homological algebra can be applied to stable homotopy-theory. In this application, we deal with A -modules, where A is the mod p Steenrod algebra. To obtain a concrete geometrical result by this method usually involves work of two distinct sorts. To illustrate this, we consider the spectral sequence of (1,2):

Here each group Extss, t which occurs in the E2 term can be effectively computed; the process is purely algebraic. However, no such effective method is given for computing the differentials dr in the spectral sequence, or for determining the group extensions by which is built up from the E∞ term; these are topological problems.

Improved sufficient conditions are developed for the functional completeness of a set F of functions with variables and values ranging over N = {1, 2, …, n}, where n ≥ 3. In particular, F is complete if it generates a triply transitive group of permutations of N and contains either (i) only a single function, or (ii) at least one function satisfying the Slupecki conditions, the latter apart from certain exceptional cases. These are shown by a detailed investigation to occur only when n = 3 or when n is a power of 2 and all functions of F are linear in each variable, relative to some representation of N as a vector space over Z2.

1. Let E be a finite non-null set and write (E) for the family of all permutations of E. Let be a non-null subset of (E) and write () for the subgroup of (E) generated by the members of . For any α ∈ we put

so that () is a subgroup of () and is independent of the choice of α in . We suppose that E splits into k disjoint transitivity sets (orbits) Ei(1 ≤ i ≤ k) with respect to (); thus σEi = Ei for all σ ∈ ().

This note gives homotopy-theoretic criteria in the metastable range for an (n + l)-manifold with boundary to be diffeomorphic to the total space of an l-disc bundle over a closed n-manifold and for two such structures to be equivalent. The results are similar to some theorems of (8) and the main technique used in the proofs is surgery on a map ((l), pp. 42–46, (7), (10)). All manifolds will be smooth.

Summary of results. In this paper we shall study some properties of the algebra A(Rn) for n ≥ 1 relative to the unit sphere

Introduction. In his paper ((1)), Baumslag has shown that the wreath product A wr B of a group A by a group B is nilpotent if and only if A is a nilpotent p-group of finite exponent and B is a finite p-group, the prime p being the same for both groups. Liebeck ((3)) has obtained the exact nilpotency class of A wr B when A and B are Abelian. Let A be an Abelian p -group of exponent pn and let B be a direct product of cyclic groups, whose orders are pβ1, …, pβn, with β1 ≤ β2 ≤ … βn. Then A wr B has nilpotency class .

In (3) W. Gaschütz introduced the concept of a formation of finite soluble groups, generalizing the results of R. W. Carter on the existence and conjugacy of nilpotent self-normalizing subgroups in finite soluble groups (2). Carter's results have already been extended to two classes of infinite groups in (9), (10), and the object of the present work is to extend the results of Gaschütz to a class of infinite groups, thereby generalizing (9).