Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gallian, Joseph A.
and
Marttila, Charles A.
1980.
Reorienting regularn-gons.
Aequationes Mathematicae,
Vol. 20,
Issue. 1,
p.
97.
Housman, David
1981.
Enumeration of hamiltonian paths in Cayley diagrams.
Aequationes Mathematicae,
Vol. 23,
Issue. 1,
p.
80.
Witte, David S.
1982.
On Hamiltonian circuits in Cayley diagrams.
Discrete Mathematics,
Vol. 38,
Issue. 1,
p.
99.
Keating, Kevin
1982.
The conjunction of Cayley digraphs.
Discrete Mathematics,
Vol. 42,
Issue. 2-3,
p.
209.
Penn, Laurence E.
and
Witte, David
1983.
When the cartesian product of two directed cycles is hypo‐Hamiltonian.
Journal of Graph Theory,
Vol. 7,
Issue. 4,
p.
441.
Witte, David
and
Gallian, Joseph A.
1984.
A survey: Hamiltonian cycles in Cayley graphs.
Discrete Mathematics,
Vol. 51,
Issue. 3,
p.
293.
Letzter, Gail
1985.
Annals of Discrete Mathematics (27): Cycles in Graphs.
Vol. 115,
Issue. ,
p.
103.
Berndt, Bruce C.
Kohnen, Winfried
and
Ono, Ken
2003.
Number Theory and Modular Forms.
Vol. 10,
Issue. ,
p.
9.
Konstantinova, Elena
2008.
Some problems on Cayley graphs.
Linear Algebra and its Applications,
Vol. 429,
Issue. 11-12,
p.
2754.
Pak, Igor
and
Radoičić, Radoš
2009.
Hamiltonian paths in Cayley graphs.
Discrete Mathematics,
Vol. 309,
Issue. 17,
p.
5501.
Ghorbani, Modjtaba
and
Larki, Farzaneh Nowroozi
2018.
On the spectrum of finite Cayley graphs.
Journal of Discrete Mathematical Sciences and Cryptography,
Vol. 21,
Issue. 1,
p.
83.


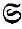 (
( be a non-null subset of
be a non-null subset of  (
(
 (
(