Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Meldrum, J. D. P.
1970.
On nilpotent wreath products.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 68,
Issue. 1,
p.
1.
Morley, Larry
1971.
Bounds on the nilpotency class of certain semidirect products.
Transactions of the American Mathematical Society,
Vol. 159,
Issue. 0,
p.
381.
Shield, David
and
Neumann, Hanna
1971.
Nilpotency and related properties of group extensions.
Bulletin of the Australian Mathematical Society,
Vol. 4,
Issue. 2,
p.
145.
Sandling, Robert
1972.
Subgroups dual to dimension subgroups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 71,
Issue. 1,
p.
33.
Chunikhin, S. A.
and
Shemetkov, L. A.
1973.
Finite groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 3,
p.
291.
Macdonald, I.D.
1973.
Computer results on Burnside groups.
Bulletin of the Australian Mathematical Society,
Vol. 9,
Issue. 3,
p.
433.
Wells, Charles
1976.
Some Applications of the Wreath Product Construction.
The American Mathematical Monthly,
Vol. 83,
Issue. 5,
p.
317.
Shield, David
1976.
Power and commutator structure of groups.
Bulletin of the Australian Mathematical Society,
Vol. 15,
Issue. 2,
p.
315.
Shakhova, N. G.
1976.
Nilpotency class of a free group of the product of certain varieties.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 19,
Issue. 1,
p.
53.
Shield, David
1977.
The class of a nilpotent wreath product.
Bulletin of the Australian Mathematical Society,
Vol. 17,
Issue. 1,
p.
53.
Zakir'yanov, K. Kh.
1983.
Index of the center of an irreducible nilpotent linear group over an algebraically closed field.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 34,
Issue. 2,
p.
568.
Riedl, Jeffrey M.
2015.
Upper central series for elementary-abelian-over-cyclic regular wreath product p-groups.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 04,
p.
1550044.
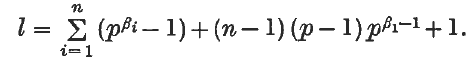 .
.