Research Article
The jet from a horizontal slot at large Froude number
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 515-529
-
- Article
- Export citation
The use of Riemann problems in solving a class of transcendental equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-118
-
- Article
- Export citation
Kolmogorov's differential equations for non-stationary, countable state Markov processes with uniformly continuous transition probabilities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-138
-
- Article
- Export citation
Front matter
PSP volume 73 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
On weak convergence of empirical processes for random number of independent stochastic vectors†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-144
-
- Article
- Export citation
Back matter
PSP volume 73 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Research Article
Positive definite functions on spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-156
-
- Article
- Export citation
Polynomial approximations to the solution of the heat equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-165
-
- Article
- Export citation
The variational derivative of degenerate Lagrange densities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-172
-
- Article
- Export citation
On isotropic tensors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 173-176
-
- Article
- Export citation
On the three-body problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 177-182
-
- Article
- Export citation
On the development of a solitary wave moving over an uneven bottom
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-203
-
- Article
- Export citation
Internal-inertia waves in a fluid of variable depth
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-213
-
- Article
- Export citation
On the structure of graded formal groups of finite characteristic
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 215-221
-
- Article
- Export citation
On the series solution to the laminar boundary layer with stationary origin on a continuous, moving porous surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-229
-
- Article
- Export citation
Low Reynolds number flow past a porous spherical shell
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-238
-
- Article
- Export citation
A further note on axially symmetric flows of elastico-viscous liquids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-247
-
- Article
- Export citation
An eigenvalue problem for elastic contact with finite friction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-268
-
- Article
- Export citation
An elastostatic circle theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-277
-
- Article
- Export citation
The polygon-circle paradox and convergence in thin plate theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 279-282
-
- Article
- Export citation

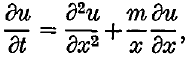
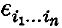 is 0 if any two of the
is 0 if any two of the 
