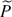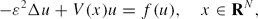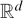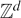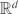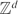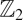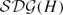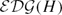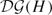Research Article
Reduced Wu and generalized Simon invariants for spatial graphs
-
- Published online by Cambridge University Press:
- 20 February 2014, pp. 521-544
-
- Article
- Export citation
Hölder differentiability of self-conformal devil's staircases
-
- Published online by Cambridge University Press:
- 09 January 2014, pp. 295-311
-
- Article
- Export citation
Ulrich ideals and modules†
-
- Published online by Cambridge University Press:
- 10 September 2013, pp. 137-166
-
- Article
- Export citation
Bott periodicity in the Hit Problem
-
- Published online by Cambridge University Press:
- 20 February 2014, pp. 545-554
-
- Article
- Export citation
On Loewy lengths of blocks
-
- Published online by Cambridge University Press:
- 20 February 2014, pp. 555-570
-
- Article
- Export citation
Semi-classical bound states of Schrödinger equations
-
- Published online by Cambridge University Press:
- 21 October 2013, pp. 167-181
-
- Article
- Export citation
Regulator of modular units and Mahler measures
-
- Published online by Cambridge University Press:
- 02 January 2014, pp. 313-326
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 156 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 25 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
The Möbius–Wall congruences for p-adic L-functions of CM elliptic curves
-
- Published online by Cambridge University Press:
- 11 November 2013, pp. 183-192
-
- Article
- Export citation
Large values of the additive energy in
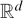 ${\mathbb{R}^d$ and
${\mathbb{R}^d$ and 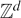 ${\mathbb{Z}^d$
${\mathbb{Z}^d$
-
- Published online by Cambridge University Press:
- 09 January 2014, pp. 327-341
-
- Article
- Export citation
The automorphism group of the
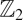 ${\mathbb Z}_2$-orbifold of the Barnes–Wall lattice vertex operator algebra of central charge 32
${\mathbb Z}_2$-orbifold of the Barnes–Wall lattice vertex operator algebra of central charge 32
-
- Published online by Cambridge University Press:
- 09 January 2014, pp. 343-361
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 156 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 December 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 156 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 25 March 2014, pp. b1-b6
-
- Article
-
- You have access
- Export citation
PSP volume 156 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 December 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Geometry of the augmented disk graph
-
- Published online by Cambridge University Press:
- 02 January 2014, pp. 363-382
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 156 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 February 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 156 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 February 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation