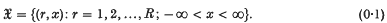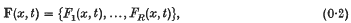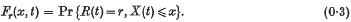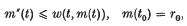Research Article
Integrals involving products of G-function and Gauss's hypergeometric function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 539-542
-
- Article
- Export citation
A continuum theory of anisotropic fluids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-128
-
- Article
- Export citation
On a class of infinite products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 847-854
-
- Article
- Export citation
Application of the Laplace transform method to wave motions involving strong discontinuities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 313-324
-
- Article
- Export citation
The development of a shock from standing waves of finite amplitude in an isentropic fluid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-135
-
- Article
- Export citation
On a problem about the Epstein zeta-function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 855-875
-
- Article
- Export citation
On the one-region two-centre expansions of a generalized Coulomb field in spherical polar and parabolic coordinates
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 543-546
-
- Article
- Export citation
Small disturbances in a conducting fluid in the presence of a current-carrying conductor
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-339
-
- Article
- Export citation
Solutions of unsteady boundary-layer equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 137-158
-
- Article
- Export citation
The Tchebysheffian approximation of one rational function by another
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 877-890
-
- Article
- Export citation
A central limit theorem for processes defined on a finite Markov chain
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 547-567
-
- Article
- Export citation
The hydromagnetics of an ellipsoid moving in a cross-field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 341-351
-
- Article
- Export citation
Differential inequalities and extension of Lyapunov's method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 891-895
-
- Article
- Export citation
Research Notes
A note on spaces with non-associative co-multiplication
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 353-354
-
- Article
- Export citation
Research Article
The stability of a system of queues in series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 569-574
-
- Article
- Export citation
The elastic stresses produced in the mid-plane of a slab by pressures applied symmetrically at its surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-169
-
- Article
- Export citation
The numerical solution of the heat conduction equation in one dimension
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 897-907
-
- Article
- Export citation
Research Notes
Continuity of homomorphisms of topological algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 171-172
-
- Article
- Export citation
Research Article
The direction of time and the equivalence of ‘expanding’ and ‘contracting’ world-models
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 575-579
-
- Article
- Export citation
Research Notes
Some embeddings of 2-spheres in 4-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 354-356
-
- Article
- Export citation

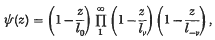
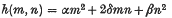
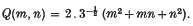
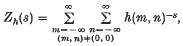
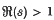 . The function
. The function