Let f{θ, φ) be a function defined for the range 0 ≤ φ π, 0 ≤ φ ≤ 2π on a sphere S. The ultraspherical series associated with this function is

where

and the ultraspherical polynomials are defined by the following expansion

.

The problem discussed is the formal solution of certain dual integral equations involving H-functions. The method followed is that of fractional integration. The given dual integral equations have been transformed, by the application of fractional integration operators, into two others with a common kernel and the problem is then reduced to solving one integral equation. In the first case the common kernel comes out to be a symmetrical Fourier kernel given earlier by Fox and the formal solution is then immediate. In the second case the common kernel is a generalized Fourier kernel and dual integral equations of this type have recently been studied by Fox.

Summary. The main result of the present paper is contained in the following: Theorem ℜ α ≠ −1, −2, −3,…

where2F1[.,.;.;.] and 1f1[.;.;.] (l).

A technique is developed for improving the speed and range of convergence of iteration procedures. The method is shown to include, as special cases, Newton's method and Aitken's δ2-acceleration process.

Introduction. Two previous papers (1,2) have dealt with additive processes defined on finite Markov chains. Such a process in discrete time may be treated as a bivariate Markov process {R(k), X(k)}. The process R(k) is an irreducible Markov chain on states r = 1, 2, …, R governed by a stochastic transition matrix B0 with components brs. The marginal process X(k) ‘defined’ on the chain R(k) is a sum 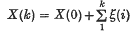of random increments ξ(i) dependent on the chain, i.e. if the ith transition takes the chain from state r to state s, ξ,(i) is chosen from a distribution function Drs(x) indexed by r and s. The distribution of the bivariate process may be represented by a vector F(x, k) with components

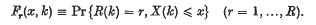
These are generated recursively by the relation

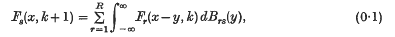
where the increment matrix distribution B(x) has components brsDrs(x). We denote the nth moment of B(x) by Bn = ∫xndB(x), so that B0 = B(∞).

In (2) a simple proof was given of the following inequality of Atkinson, Watterson and Moran (l), a slight generalization of a result of Scheuer and Mandel ((4), see also (3)) which is of importance in genetics. If aij, pi, qj (i, j = 1, 2, 3,…) are non-negative numbers with

and if

then

and if then This result is shown in (2) to be a special case of a large class of inequalities involving sets of non-negative numbers depending on several indices, and ‘partial averages’ over subsets of those indices.

The notion of a general dynamical system was introduced by Barbashin(1). In this paper we consider a general dynamical system in a metric space following Zubov(6) where Lyapunov's method has been extended to investigate the stability properties using a single Lyapunov functional.

The integral equation for the isotropic scattering of radiation in a medium bounded laterally by planes ±y0 is solved as a series in powers of exp (−y0). This series is certainly convergent for y0 large enough, and rapidly convergent for most practical purposes.

It is proved that for a second-order, homogeneous, random process on a globally symmetric space a filter, that is a closed linear operator which is invariant under a group of isometries of the space, may be fully described through a response function, that is that it has a direct integral decomposition into components which are scalar multiples of the identity.

Introduction. The distribution of stress produced in the interior of an infinite elastic solid when a constant pressure is applied over the entire surface of a penny-shaped crack has been solved by Sneddon(6), (7). The problem considered here is the closely allied one of a plane longitudinal wave, harmonic in time, moving in the positive direction of the z-axis and impinging on the surface of a penny-shaped crack. The analysis follows the methods adopted for dealing with an axisymmetrical vibrating punch acting on a semi-infinite elastic solid, Robertson (5).

The two fourth-order partial differential equations giving the transverse displacement and the stress functions for shallow shells are reduced to a sixth-order differential equation in one variable which has been solved, and the values of displacements, stress resultants and couples are all expressed in terms of Bessel Functions of imaginary argument. Numerical values of the displacement presented for points on the shell on different meridian lines, showed that on the symmetrical line deflexion is maximum at the point of loading but the point of maximum deflexion shifts gradually towards the pole.

Consider the two-dimensional irrotational steady flow of an incompressible inviscid fluid under no body forces between two infinite horizontal planes. When a vertical wall which intersects the upper plane is introduced in the flow, the fluid will flow under the wall and will be bounded above by a free streamline along which the pressure is constant. This configuration is called a sluice gate. At infinity the flow will be uniform and parallel with input velocity V and exit velocity U.

It is argued that the zero Reynolds limit of the steady incompressible axially symmetric viscous fluid motion interior to a sphere due to a Landau source at the centre is a Stokes flow. The first three terms of the perturbation expansion are determined and the order of magnitude of the general term not derivable from the Landau source is established. Comparison of the convection terms with the diffusion terms for each order of the Reynolds number demonstrates self consistency at each stage of the expansion.