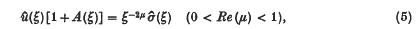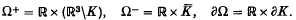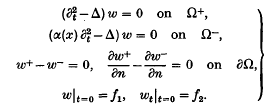Research Article
Strategies for compounds of partizan games
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-204
-
- Article
- Export citation
Osculating hyperplanes and a quartic combinant of the nonsingular model of the Kummer and Weddle surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-220
-
- Article
- Export citation
A lifting result for local cohomology of graded modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 221-229
-
- Article
- Export citation
On Ext1 for semisimple groups and infinitesimal subgroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-238
-
- Article
- Export citation
Semidirect products of central groups and groups with equal uniformities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 239-241
-
- Article
- Export citation
Isometric immersions into manifolds without conjugate points
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-250
-
- Article
- Export citation
Isomorphic embeddings of l1(Г) into subspaces of C(Ω)*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-262
-
- Article
- Export citation
On the K-theory of the extended power construction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 263-274
-
- Article
- Export citation
Real inversion theorems for generalized Stieltjes transforms. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 275-291
-
- Article
- Export citation
Asymptotic analysis of the Cooke-Noble integral equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 293-306
-
- Article
- Export citation
An extremum variational principle and error estimate procedure for qIV = f(q, x)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-316
-
- Article
- Export citation
Edth-a differential operator on the sphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 317-330
-
- Article
- Export citation
The singularities of H-space†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-347
-
- Article
- Export citation
Poisson convergence and random graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 349-359
-
- Article
- Export citation
Inverse scattering problem for transparent obstacles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 361-367
-
- Article
- Export citation
Note on the reflexion of water waves at a wall in the presence of surface tension
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-374
-
- Article
- Export citation
Corrigenda
Cobordism of homology manifolds - Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-378
-
- Article
-
- You have access
- Export citation
Transverse regularity for maps of homology manifolds - Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 379
-
- Article
-
- You have access
- Export citation
A quadratic recurrence of Faltung type - Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 379
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 92 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation