Research Article
On decomposition numbers and Alvis–Curtis duality
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 509-520
-
- Article
- Export citation
Polynomial bounds for equivalence of quadratic forms with cube-free determinant
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 521-532
-
- Article
- Export citation
On factorials which are products of factorials
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 533-542
-
- Article
- Export citation
On motivic principal value integrals
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 543-555
-
- Article
- Export citation
Geometric collections and Castelnuovo–Mumford regularity
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 557-578
-
- Article
- Export citation
On Manin's conjecture for singular del Pezzo surfaces of degree four, II
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 579-605
-
- Article
- Export citation
Stable sandwich classification theorem for classical-like groups
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 607-619
-
- Article
- Export citation
Bridge numbers of torus knots
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 621-625
-
- Article
- Export citation
The second Johnson homomorphism and the second rational cohomology of the Johnson kernel
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 627-648
-
- Article
- Export citation
Lehmer's Question, Knots and Surface Dynamics
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 649-661
-
- Article
- Export citation
There exist conjugate simple braids whose associated permutations are not strongly conjugate
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 663-667
-
- Article
- Export citation
Integral bases for certain TQFT-modules of the torus
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 669-684
-
- Article
- Export citation
Sectorial forms and unbounded subnormals
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 685-702
-
- Article
- Export citation
Uniqueness of spacelike hypersurfaces with constant higher order mean curvature in generalized Robertson–Walker spacetimes
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 703-729
-
- Article
- Export citation
Self-gravitating stationary spherically symmetric systems in relativistic galactic dynamics
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 731-752
-
- Article
- Export citation
Proceedings of Meetings
Proceedings of the meetings held during the session 2006–2007
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 753-760
-
- Article
- Export citation


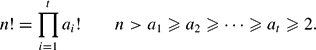
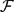 on a smooth projective variety with a geometric collection, two spectral sequences: the first one abuts to
on a smooth projective variety with a geometric collection, two spectral sequences: the first one abuts to 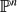 and for a suitable geometric collection of coherent sheaves on
and for a suitable geometric collection of coherent sheaves on 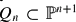 (
(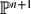 .
.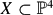 . In fact, if
. In fact, if 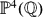 , then the height zeta function
, then the height zeta function 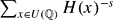 is analytically continued to the half-plane ℜ
is analytically continued to the half-plane ℜ