On the assumption of the Riemann hypothesis and a spacing hypothesis for the nontrivial zeros 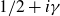 $1/2+i\gamma$ of the Riemann zeta function, we show that the sequence
$1/2+i\gamma$ of the Riemann zeta function, we show that the sequence
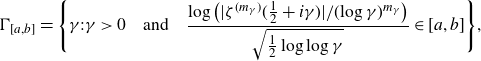 \begin{equation*}\Gamma_{[a, b]} =\Bigg\{ \gamma : \gamma>0 \quad \mbox{and} \quad \frac{ \log\big(| \zeta^{(m_{\gamma })} (\frac12+ i{\gamma }) | / (\!\log{{\gamma }} )^{m_{\gamma }}\big)}{\sqrt{\frac12\log\log {\gamma }}} \in [a, b] \Bigg\},\end{equation*}
\begin{equation*}\Gamma_{[a, b]} =\Bigg\{ \gamma : \gamma>0 \quad \mbox{and} \quad \frac{ \log\big(| \zeta^{(m_{\gamma })} (\frac12+ i{\gamma }) | / (\!\log{{\gamma }} )^{m_{\gamma }}\big)}{\sqrt{\frac12\log\log {\gamma }}} \in [a, b] \Bigg\},\end{equation*}where the
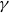 ${\gamma }$
${\gamma }$ are arranged in increasing order, is uniformly distributed modulo one. Here
a and
b are real numbers with
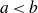 $a<b$
$a<b$, and
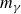 $m_\gamma$
$m_\gamma$ denotes the multiplicity of the zero
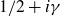 $1/2+i{\gamma }$
$1/2+i{\gamma }$. The same result holds when the
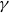 ${\gamma }$
${\gamma }$’s are restricted to be the ordinates of simple zeros. With an extra hypothesis, we are also able to show an equidistribution result for the scaled numbers
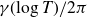 $\gamma (\!\log T)/2\pi$
$\gamma (\!\log T)/2\pi$ with
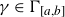 ${\gamma }\in \Gamma_{[a, b]}$
${\gamma }\in \Gamma_{[a, b]}$ and
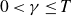 $0<{\gamma }\leq T$
$0<{\gamma }\leq T$.