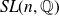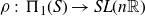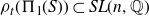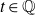1. Introduction
Constructing Zariski dense surface subgroups in
![]() $SL(n,\mathbb{R})$
has attracted attention as a step to finding thin groups, these are infinite index subgroups of a lattice in
$SL(n,\mathbb{R})$
has attracted attention as a step to finding thin groups, these are infinite index subgroups of a lattice in
![]() $SL(n,\mathbb{R})$
which are Zariski dense. Finding thin subgroups inside lattices in a variety of Lie groups has been a topic of significant interest in recent years, in part from the connections thin groups have to expanders and the affine sieve of Bourgain, Gamburd and Sarnak [
Reference Bourgain, Gamburd and SarnakBGS10, Reference SarnakSar14
].
$SL(n,\mathbb{R})$
which are Zariski dense. Finding thin subgroups inside lattices in a variety of Lie groups has been a topic of significant interest in recent years, in part from the connections thin groups have to expanders and the affine sieve of Bourgain, Gamburd and Sarnak [
Reference Bourgain, Gamburd and SarnakBGS10, Reference SarnakSar14
].
Though thin subgroups are in a sense generic [
Reference FuchsFuc14, Reference Fuchs and RivinFR17
], finding particular specimens of thin surface subgroups in a given lattice remains a difficult task. In this direction, in 2011 Long, Reid and Thistlethwaite [
Reference Long, Reid and ThistlethwaiteLRT11
] produced the first infinite family of nonconjugate thin surface groups in
![]() $SL(3,\mathbb{Z})$
. Their approach relies on parametrising a family of representations
$SL(3,\mathbb{Z})$
. Their approach relies on parametrising a family of representations
![]() $\rho_t$
of the triangle group
$\rho_t$
of the triangle group
![]() $\Delta(3,3,4)$
in the Hitchin component, so that for every
$\Delta(3,3,4)$
in the Hitchin component, so that for every
![]() $t\in \mathbb{Z}$
the subgroup
$t\in \mathbb{Z}$
the subgroup
![]() $\rho_t(\Delta(3,3,4))$
is in
$\rho_t(\Delta(3,3,4))$
is in
![]() $SL(3,\mathbb{Q})$
and has integral traces. By results of Bass [
Reference BassBas80
] these two properties together with
$SL(3,\mathbb{Q})$
and has integral traces. By results of Bass [
Reference BassBas80
] these two properties together with
![]() $\rho_t(\Delta(3,3,4))$
being non-solvable and finitely generated guarantee that it is conjugate to a subgroup of
$\rho_t(\Delta(3,3,4))$
being non-solvable and finitely generated guarantee that it is conjugate to a subgroup of
![]() $SL(3,\mathbb{Z})$
. In 2018 Long and Thistlethwaite [
Reference Long and ThistlethwaiteLT18
] used a similar approach to obtain an infinite family of non-conjugate Zariski dense surface subgroups in
$SL(3,\mathbb{Z})$
. In 2018 Long and Thistlethwaite [
Reference Long and ThistlethwaiteLT18
] used a similar approach to obtain an infinite family of non-conjugate Zariski dense surface subgroups in
![]() $SL(4,\mathbb{Z})$
and
$SL(4,\mathbb{Z})$
and
![]() $SL(5,\mathbb{Z})$
.
$SL(5,\mathbb{Z})$
.
Ballas and Long [
Reference Ballas and LongBL18
] in turn used the idea of “bending” a representation of the fundamental group of a hyperbolic n-manifold
![]() $\pi_1(N)$
along an embedded totally geodesic and separating hypersurface to obtain thin groups in
$\pi_1(N)$
along an embedded totally geodesic and separating hypersurface to obtain thin groups in
![]() $SL(n+1,\mathbb{R})$
which are isomorphic to
$SL(n+1,\mathbb{R})$
which are isomorphic to
![]() $\pi_1(N)$
. The aim of this paper is to combine the aforementioned approaches to construct a family of Zariski dense rational surface group representations by bending orbifold representations. Our main result is the following:
$\pi_1(N)$
. The aim of this paper is to combine the aforementioned approaches to construct a family of Zariski dense rational surface group representations by bending orbifold representations. Our main result is the following:
Theorem 1. For every surface S finitely covering the orbifold
![]() ${\mathcal{O}}_{3,3,3,3}$
and every odd
${\mathcal{O}}_{3,3,3,3}$
and every odd
![]() $n>1$
there exists a path of discrete, faithful and irreducible representations
$n>1$
there exists a path of discrete, faithful and irreducible representations
![]() $\rho_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
, so that:
$\rho_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
, so that:
-
(i)
 $\rho_0(\pi_1(S)) < SL(n,\mathbb{Z})$
;
$\rho_0(\pi_1(S)) < SL(n,\mathbb{Z})$
; -
(ii)
 $\rho_t$
is Zariski dense for every
$\rho_t$
is Zariski dense for every
 $t>0$
; and
$t>0$
; and -
(iii)
 $\rho_t(\pi_1(S)) < SL(n,\mathbb{Q})$
for every
$\rho_t(\pi_1(S)) < SL(n,\mathbb{Q})$
for every
 $t\in \mathbb{Q}$
.
$t\in \mathbb{Q}$
.
Every representation
![]() $\rho_t$
in Theorem 1 is a surface Hitchin representation. Several of its properties are derived from the seminal work of Labourie [
Reference LabourieLab06
] on Anosov representations, the classification of Zariski closures of surface Hitchin representations by Guichard [
Reference GuichardGui
], and the recent introduction of orbifold Hitchin representations by Alessandrini, Lee and Schaffhauser [
Reference Alessandrini, Lee and SchaffhauserALS19
]. We provide an overview of these results in Sections 2 and 3. The discussion in these sections applies to all n, with the assumption of odd n coming into play later in Section 4. At the end of Section 3 we also prove the following criterion for Zariski density, which will be subsequently used to discard Zariski closures.
$\rho_t$
in Theorem 1 is a surface Hitchin representation. Several of its properties are derived from the seminal work of Labourie [
Reference LabourieLab06
] on Anosov representations, the classification of Zariski closures of surface Hitchin representations by Guichard [
Reference GuichardGui
], and the recent introduction of orbifold Hitchin representations by Alessandrini, Lee and Schaffhauser [
Reference Alessandrini, Lee and SchaffhauserALS19
]. We provide an overview of these results in Sections 2 and 3. The discussion in these sections applies to all n, with the assumption of odd n coming into play later in Section 4. At the end of Section 3 we also prove the following criterion for Zariski density, which will be subsequently used to discard Zariski closures.
Proposition 2. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
be an orbifold Hitchin representation such that:
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
be an orbifold Hitchin representation such that:
if
![]() $n=2k$
is even then
$n=2k$
is even then
![]() $\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
$\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
![]() $PSp(2k,\mathbb{R})$
or,
$PSp(2k,\mathbb{R})$
or,
if
![]() $n=2k+1$
is odd then
$n=2k+1$
is odd then
![]() $\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
$\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
![]() $PSO(k,k+1)$
.
$PSO(k,k+1)$
.
Then
![]() $\rho(H)$
is Zariski dense in
$\rho(H)$
is Zariski dense in
![]() $PSL(n,\mathbb{R})$
for every finite index subgroup H of
$PSL(n,\mathbb{R})$
for every finite index subgroup H of
![]() $\pi_1({\mathcal{O}})$
.
$\pi_1({\mathcal{O}})$
.
In Section 4 we give a general construction to obtain a path of representations as in Theorem 1. This is based on bending the fundamental group
![]() $\pi_1({\mathcal{O}})$
of a hyperbolic 2-dimensional orbifold along a simple closed curve in
$\pi_1({\mathcal{O}})$
of a hyperbolic 2-dimensional orbifold along a simple closed curve in
![]() ${\mathcal{O}}$
with infinite order as an element of
${\mathcal{O}}$
with infinite order as an element of
![]() $\pi_1({\mathcal{O}})$
. Theorem 1 then follows from applying the results in Section 2 to a suitable representation of the fundamental group of the orbifold
$\pi_1({\mathcal{O}})$
. Theorem 1 then follows from applying the results in Section 2 to a suitable representation of the fundamental group of the orbifold
![]() ${\mathcal{O}}_{3,3,3,3}$
whose underlying topological space is
${\mathcal{O}}_{3,3,3,3}$
whose underlying topological space is
![]() $S^2$
and has four cone points of order 3. This final step is covered in Section 5.
$S^2$
and has four cone points of order 3. This final step is covered in Section 5.
Remark. During the finalisation of this project, Long and Thistlethwaite used bending to construct thin surface groups in
![]() $SL(n,\mathbb{Z})$
for every odd n [
Reference Long and ThistlethwaiteLT20
], the even case remains open.
$SL(n,\mathbb{Z})$
for every odd n [
Reference Long and ThistlethwaiteLT20
], the even case remains open.
2. Hitchin representations
In this section we give a short overview of surface and orbifold Hitchin representations.
Recall that a subgroup
![]() $H<GL(n,\mathbb{R})$
is irreducible if the only invariant subspaces for the action of H on
$H<GL(n,\mathbb{R})$
is irreducible if the only invariant subspaces for the action of H on
![]() $\mathbb{R}^n$
are
$\mathbb{R}^n$
are
![]() $\{0\}$
and
$\{0\}$
and
![]() $\mathbb{R}^n$
. A representation
$\mathbb{R}^n$
. A representation
![]() $\rho: \Gamma \to GL(n,\mathbb{R})$
is said to be irreducible if the image subgroup
$\rho: \Gamma \to GL(n,\mathbb{R})$
is said to be irreducible if the image subgroup
![]() $\rho(\Gamma)$
is irreducible, and it is strongly irreducible if the restriction of
$\rho(\Gamma)$
is irreducible, and it is strongly irreducible if the restriction of
![]() $\rho$
to every finite index subgroup is irreducible. These characteristics are defined similarly for projective representations
$\rho$
to every finite index subgroup is irreducible. These characteristics are defined similarly for projective representations
![]() $\rho\;:\;\thinspace\Gamma \to PGL(n,\mathbb{R})$
$\rho\;:\;\thinspace\Gamma \to PGL(n,\mathbb{R})$
2·1. Spaces of representations
Let G be a Lie group and let
![]() $\Gamma$
be a group with a finite presentation
$\Gamma$
be a group with a finite presentation
![]() $\langle \alpha_1, \ldots, \alpha_k \ | \ r_1, \ldots , r_m \rangle$
. Then every relator
$\langle \alpha_1, \ldots, \alpha_k \ | \ r_1, \ldots , r_m \rangle$
. Then every relator
![]() $r_i$
defines a map
$r_i$
defines a map
![]() $R_i \;:\;\thinspace G^k \to G$
. If we let
$R_i \;:\;\thinspace G^k \to G$
. If we let
![]() $\text{Hom}(\Gamma, G) = \cap_{i=1}^m R_i^{-1}(Id)$
, then the map
$\text{Hom}(\Gamma, G) = \cap_{i=1}^m R_i^{-1}(Id)$
, then the map
![]() $\phi \mapsto (\phi(\alpha_1), \ldots, \phi(\alpha_k))$
is a bijection between the set of all group homomorphisms from
$\phi \mapsto (\phi(\alpha_1), \ldots, \phi(\alpha_k))$
is a bijection between the set of all group homomorphisms from
![]() $\Gamma$
to G and
$\Gamma$
to G and
![]() $\text{Hom}(\Gamma, G)$
. We will regard
$\text{Hom}(\Gamma, G)$
. We will regard
![]() $\text{Hom}(\Gamma, G)$
as having the subspace topology from
$\text{Hom}(\Gamma, G)$
as having the subspace topology from
![]() $G^k$
.
$G^k$
.
Let
![]() $\text{Hom}^+(\Gamma, G)$
be the subset of representations in
$\text{Hom}^+(\Gamma, G)$
be the subset of representations in
![]() $\text{Hom}(\Gamma,G)$
which decompose as a direct sum of irreducible representations and let
$\text{Hom}(\Gamma,G)$
which decompose as a direct sum of irreducible representations and let
![]() $\text{Rep}^+(\Gamma, G) = \text{Hom}^+(\Gamma,G)/G$
be the quotient space by the conjugation action. With the quotient topology
$\text{Rep}^+(\Gamma, G) = \text{Hom}^+(\Gamma,G)/G$
be the quotient space by the conjugation action. With the quotient topology
![]() $\text{Rep}^+(\Gamma, G)$
has the structure of an algebraic variety [
Reference Bradlow, Garca-Prad, Goldman and WienhardBGPGW07
, section 5·2].
$\text{Rep}^+(\Gamma, G)$
has the structure of an algebraic variety [
Reference Bradlow, Garca-Prad, Goldman and WienhardBGPGW07
, section 5·2].
In the following we will frequently use the representation
given by the action of
![]() $SL(2,\mathbb{R})$
on the vector space
$SL(2,\mathbb{R})$
on the vector space
![]() $\mathcal{P}$
of homogeneous polynomials in 2 variables of degree
$\mathcal{P}$
of homogeneous polynomials in 2 variables of degree
![]() $n-1$
. It is known that the representation
$n-1$
. It is known that the representation
![]() $\tilde\omega_n$
is absolutely irreducible and is, up to conjugation, the unique irreducible representation from
$\tilde\omega_n$
is absolutely irreducible and is, up to conjugation, the unique irreducible representation from
![]() $SL(2,\mathbb{R})$
into
$SL(2,\mathbb{R})$
into
![]() $SL(n,\mathbb{R})$
. This representation induces a projective representation
$SL(n,\mathbb{R})$
. This representation induces a projective representation
![]() $\omega_n \;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
which is also irreducible and unique up to conjugation.
$\omega_n \;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
which is also irreducible and unique up to conjugation.
2·2. Hitchin representations of surface groups
Let S be a closed surface of genus
![]() $g>1$
. In 1988 Goldman proved that
$g>1$
. In 1988 Goldman proved that
![]() $\text{Rep}^+(\pi_1(S),PSL(2,\mathbb{R}))$
has
$\text{Rep}^+(\pi_1(S),PSL(2,\mathbb{R}))$
has
![]() $4g-3$
connected components, two of which are diffeomorphic to
$4g-3$
connected components, two of which are diffeomorphic to
![]() $\mathbb{R}^{6g-6}$
and called these Teichmüller spaces [
Reference GoldmanGol88
, theorem A] [
Reference HitchinHit92
, theorem 10·2]. The two Teichmüller spaces
$\mathbb{R}^{6g-6}$
and called these Teichmüller spaces [
Reference GoldmanGol88
, theorem A] [
Reference HitchinHit92
, theorem 10·2]. The two Teichmüller spaces
![]() $\mathcal{T}^\pm(S)$
are precisely the sets of conjugacy classes by
$\mathcal{T}^\pm(S)$
are precisely the sets of conjugacy classes by
![]() $PSL(2,\mathbb{R})$
of Fuchsian representations, which are discrete and faithful representations
$PSL(2,\mathbb{R})$
of Fuchsian representations, which are discrete and faithful representations
![]() $\rho\;:\;\thinspace \pi_1(S) \to PSL(2,\mathbb{R})\equiv\text{Isom}^+(\mathbb{H}^{2} )$
.
$\rho\;:\;\thinspace \pi_1(S) \to PSL(2,\mathbb{R})\equiv\text{Isom}^+(\mathbb{H}^{2} )$
.
Definition 3. For
![]() $n>2$
a representation
$n>2$
a representation
![]() $r\;:\;\thinspace \pi_1(S) \to PSL(n,\mathbb{R})$
is called Fuchsian if it can be decomposed as
$r\;:\;\thinspace \pi_1(S) \to PSL(n,\mathbb{R})$
is called Fuchsian if it can be decomposed as
![]() $r = \omega_n\circ r_0$
where
$r = \omega_n\circ r_0$
where
![]() $r_0\;:\;\thinspace \pi_1(S)\to PSL(2,\mathbb{R})$
is discrete and faithful, and
$r_0\;:\;\thinspace \pi_1(S)\to PSL(2,\mathbb{R})$
is discrete and faithful, and
![]() $\omega_n\;:\;\thinspace PSL(2,\mathbb{R})\to PSL(n,\mathbb{R})$
is the unique irreducible representation introduced in Section 2·1.
$\omega_n\;:\;\thinspace PSL(2,\mathbb{R})\to PSL(n,\mathbb{R})$
is the unique irreducible representation introduced in Section 2·1.
Definition 4. The Fuchsian locus is the set of all
![]() $PSL(n,\mathbb{R})$
conjugacy classes of Fuchsian representations, namely the set
$PSL(n,\mathbb{R})$
conjugacy classes of Fuchsian representations, namely the set
![]() $\omega_n(\mathcal{T}^\pm(S))$
.
$\omega_n(\mathcal{T}^\pm(S))$
.
The space
![]() $\text{Rep}^+(\pi_1(S), PSL(n,\mathbb{R}))$
has three topological connected components if n is odd and 6 if n is even [
Reference HitchinHit92
, theorem 10·2]. The Fuchsian locus is contained in one component in the odd case and in two components in the even case. Each of these distinguished components, called Hitchin components, is diffeomorphic to
$\text{Rep}^+(\pi_1(S), PSL(n,\mathbb{R}))$
has three topological connected components if n is odd and 6 if n is even [
Reference HitchinHit92
, theorem 10·2]. The Fuchsian locus is contained in one component in the odd case and in two components in the even case. Each of these distinguished components, called Hitchin components, is diffeomorphic to
![]() $\mathbb{R}^{(1-n^2)(1-g)}$
. When
$\mathbb{R}^{(1-n^2)(1-g)}$
. When
![]() $n>2$
is even, both Hitchin components are related by an inner automorphism of
$n>2$
is even, both Hitchin components are related by an inner automorphism of
![]() $PSL(n,\mathbb{R})$
. In the odd case, where there is only one component, we will denote the Hitchin component by
$PSL(n,\mathbb{R})$
. In the odd case, where there is only one component, we will denote the Hitchin component by
![]() $\text{Hit}(\pi_1(S),PSL(n,\mathbb{R}))$
.
$\text{Hit}(\pi_1(S),PSL(n,\mathbb{R}))$
.
Definition 5. Let S be a closed surface of genus greater than one. A representation
![]() $r \;:\;\thinspace \pi_1(S) \to PSL(n,\mathbb{R})$
is a surface Hitchin representation if its
$r \;:\;\thinspace \pi_1(S) \to PSL(n,\mathbb{R})$
is a surface Hitchin representation if its
![]() $PSL(n,\mathbb{R})$
-conjugacy class belongs to a Hitchin component of
$PSL(n,\mathbb{R})$
-conjugacy class belongs to a Hitchin component of
![]() $\text{Rep}^+(\pi_1(S),PSL(n,\mathbb{R}))$
.
$\text{Rep}^+(\pi_1(S),PSL(n,\mathbb{R}))$
.
In [
Reference LabourieLab06
], Labourie introduces Anosov representations and proves that surface Hitchin representations are B-Anosov where B is any Borel subgroup of
![]() $PSL(n,\mathbb{R})$
. This gives surface Hitchin representations essential algebraic properties, out of which we will use Theorem 7 below.
$PSL(n,\mathbb{R})$
. This gives surface Hitchin representations essential algebraic properties, out of which we will use Theorem 7 below.
Definition 6 ([
Reference Bridgeman, Canary and LabourieBCL20
, section 2·2]). A matrix
![]() $A\in SL(n,\mathbb{R})$
is purely loxodromic if it is diagonalizable over
$A\in SL(n,\mathbb{R})$
is purely loxodromic if it is diagonalizable over
![]() $\mathbb{R}$
with eigenvalues of distinct modulus. If
$\mathbb{R}$
with eigenvalues of distinct modulus. If
![]() $A \in PSL(n,\mathbb{R})$
then we say A is purely loxodromic if any lift of A to an element of
$A \in PSL(n,\mathbb{R})$
then we say A is purely loxodromic if any lift of A to an element of
![]() $SL(n,\mathbb{R})$
is purely loxodromic.
$SL(n,\mathbb{R})$
is purely loxodromic.
Theorem 7 ([
Reference LabourieLab06
, theorem 1·5, lemma 10·1]). A surface Hitchin representation
![]() $r\;:\;\thinspace \pi_1(S) \to PSL(n,\mathbb{R})$
is discrete, faithful and strongly irreducible. Moreover, the image of every non-trivial element of
$r\;:\;\thinspace \pi_1(S) \to PSL(n,\mathbb{R})$
is discrete, faithful and strongly irreducible. Moreover, the image of every non-trivial element of
![]() $\pi_1(S)$
under r is purely loxodromic.
$\pi_1(S)$
under r is purely loxodromic.
2·3. Hitchin representations of orbifold groups
Let
![]() ${\mathcal{O}}$
be a 2-dimensional closed orbifold of negative orbifold Euler characteristic
${\mathcal{O}}$
be a 2-dimensional closed orbifold of negative orbifold Euler characteristic
![]() $\chi({\mathcal{O}})$
and let
$\chi({\mathcal{O}})$
and let
![]() $\pi_1({\mathcal{O}})$
be its orbifold fundamental group. In [
Reference ThurstonThu78
] Thurston proves there is a connected component of the representation space
$\pi_1({\mathcal{O}})$
be its orbifold fundamental group. In [
Reference ThurstonThu78
] Thurston proves there is a connected component of the representation space
![]() $\text{Rep}(\pi_1({\mathcal{O}}), PGL(2,\mathbb{R}))$
that parametrizes hyperbolic structures on
$\text{Rep}(\pi_1({\mathcal{O}}), PGL(2,\mathbb{R}))$
that parametrizes hyperbolic structures on
![]() ${\mathcal{O}}$
. This component is called the Teichmüller space of the orbifold
${\mathcal{O}}$
. This component is called the Teichmüller space of the orbifold
![]() ${\mathcal{O}}$
, we will denote it by
${\mathcal{O}}$
, we will denote it by
![]() $\mathcal{T}({\mathcal{O}})$
. As with surfaces, the orbifold Teichmüller space consists of conjugacy classes of discrete and faithful representations of
$\mathcal{T}({\mathcal{O}})$
. As with surfaces, the orbifold Teichmüller space consists of conjugacy classes of discrete and faithful representations of
![]() $\pi_1({\mathcal{O}})$
into
$\pi_1({\mathcal{O}})$
into
![]() $PGL(2,\mathbb{R}) \equiv \text{Isom}(\mathbb{H}^{2} )$
, which we will call Fuchsian representations too. More recently, Alessandrini, Lee, and Schaffhauser used the irreducible representation
$PGL(2,\mathbb{R}) \equiv \text{Isom}(\mathbb{H}^{2} )$
, which we will call Fuchsian representations too. More recently, Alessandrini, Lee, and Schaffhauser used the irreducible representation
![]() $\omega_n$
to define the Hitchin component
$\omega_n$
to define the Hitchin component
![]() $\text{Hit}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
of
$\text{Hit}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
of
![]() $\text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
as the unique connected component in this representation space which contains the connected Fuchsian locus
$\text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
as the unique connected component in this representation space which contains the connected Fuchsian locus
![]() $\omega_n(\mathcal{T}({\mathcal{O}}))$
[
Reference Alessandrini, Lee and SchaffhauserALS19
, definition 2·3] and prove
$\omega_n(\mathcal{T}({\mathcal{O}}))$
[
Reference Alessandrini, Lee and SchaffhauserALS19
, definition 2·3] and prove
![]() $\text{Hit}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
is homeomorphic to an open ball [
Reference Alessandrini, Lee and SchaffhauserALS19
, theorem 1·2].
$\text{Hit}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
is homeomorphic to an open ball [
Reference Alessandrini, Lee and SchaffhauserALS19
, theorem 1·2].
Definition 8 ([
Reference Alessandrini, Lee and SchaffhauserALS19
, definition 2·4]). Let
![]() ${\mathcal{O}}$
be a 2-dimensional connected closed orbifold with negative orbifold Euler characteristic. A representation
${\mathcal{O}}$
be a 2-dimensional connected closed orbifold with negative orbifold Euler characteristic. A representation
![]() $r\;:\;\thinspace \pi_1({\mathcal{O}}) \to PGL(n,\mathbb{R})$
is an orbifold Hitchin representation if its
$r\;:\;\thinspace \pi_1({\mathcal{O}}) \to PGL(n,\mathbb{R})$
is an orbifold Hitchin representation if its
![]() $PGL(n,\mathbb{R})$
-conjugacy class belongs to the Hitchin component
$PGL(n,\mathbb{R})$
-conjugacy class belongs to the Hitchin component
![]() $\text{Hit}(\pi_1({\mathcal{O}}), PGL(n,\mathbb{R}))$
of
$\text{Hit}(\pi_1({\mathcal{O}}), PGL(n,\mathbb{R}))$
of
![]() $\text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
.
$\text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
.
The definition of Anosov representations has been generalized by Guichard and Wienhard [
Reference Guichard and WienhardGW12
, definition 2·10] to include representations of word hyperbolic groups into semisimple Lie groups. With this more general definition, and just as their surface counterparts, orbifold Hitchin representations are also B-Anosov where B is a Borel subgroup of
![]() $PGL(n,\mathbb{R})$
[
Reference Alessandrini, Lee and SchaffhauserALS19
, proposition 2·26] and thus share some strong algebraic properties.
$PGL(n,\mathbb{R})$
[
Reference Alessandrini, Lee and SchaffhauserALS19
, proposition 2·26] and thus share some strong algebraic properties.
Theorem 9 ([
Reference Alessandrini, Lee and SchaffhauserALS19
, theorem 1·1]). An orbifold Hitchin representation
![]() $r\;:\;\thinspace \pi_1({\mathcal{O}}) \to PGL(n,\mathbb{R})$
is discrete, faithful and strongly irreducible. Moreover, the image of every infinite order element of
$r\;:\;\thinspace \pi_1({\mathcal{O}}) \to PGL(n,\mathbb{R})$
is discrete, faithful and strongly irreducible. Moreover, the image of every infinite order element of
![]() $\pi_1({\mathcal{O}})$
under r is purely loxodromic.
$\pi_1({\mathcal{O}})$
under r is purely loxodromic.
3. Zariski dense Hitchin representations
In this section we focus on Zariski density of Hitchin representations and prove Corollary 15 which gives a criterion to determine when the image of a finite index subgroup of an orbifold group under a Hitchin representation is Zariski dense.
3·1. Zariski closures of Hitchin representations
Let G be an algebraic matrix Lie group, then G has both its standard topology as a subset of some
![]() $\mathbb{R}^N$
and the Zariski topology. If X is a subset of G then its Zariski closure is the closure of X in G with respect to the Zariski topology. We say a subgroup
$\mathbb{R}^N$
and the Zariski topology. If X is a subset of G then its Zariski closure is the closure of X in G with respect to the Zariski topology. We say a subgroup
![]() $H<G$
is Zariski dense in G if its Zariski closure equals G. A representation
$H<G$
is Zariski dense in G if its Zariski closure equals G. A representation
![]() $r\;:\;\thinspace \Gamma \to G$
is Zariski dense if
$r\;:\;\thinspace \Gamma \to G$
is Zariski dense if
![]() $r(\Gamma)$
is Zariski dense in G.
$r(\Gamma)$
is Zariski dense in G.
The image of the irreducible representation
![]() $\omega_n\;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
is contained, if n is even, in a conjugate of
$\omega_n\;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
is contained, if n is even, in a conjugate of
![]() $PSp(n, \mathbb{R})$
, which is the projectivisation of the symplectic group
$PSp(n, \mathbb{R})$
, which is the projectivisation of the symplectic group
![]() $Sp(n, \mathbb{R})$
. If
$Sp(n, \mathbb{R})$
. If
![]() $n = 2k + 1$
is odd, the image of
$n = 2k + 1$
is odd, the image of
![]() $\omega_n$
is contained in a conjugate of the orthogonal group
$\omega_n$
is contained in a conjugate of the orthogonal group
![]() $SO(k, k + 1) = PSO(k,k+1)$
. This implies that the images of Fuchsian representations are contained in (a conjugate of)
$SO(k, k + 1) = PSO(k,k+1)$
. This implies that the images of Fuchsian representations are contained in (a conjugate of)
![]() $PSp(n,\mathbb{R})$
or in
$PSp(n,\mathbb{R})$
or in
![]() $SO(k,k+1)$
and, in particular, they are not Zariski dense. More generally, for surface Hitchin representations Guichard [
Reference GuichardGui
] has announced a classification of Zariski closures of their lifts. An alternative proof of this result has been given recently by Sambarino [
Reference SambarinoSam20
, corallary 1·5] The version of this result we cite here comes from theorem 11·7 in [
Reference Bridgeman, Canary, Labourie and SambarinoBCLS15
].
$SO(k,k+1)$
and, in particular, they are not Zariski dense. More generally, for surface Hitchin representations Guichard [
Reference GuichardGui
] has announced a classification of Zariski closures of their lifts. An alternative proof of this result has been given recently by Sambarino [
Reference SambarinoSam20
, corallary 1·5] The version of this result we cite here comes from theorem 11·7 in [
Reference Bridgeman, Canary, Labourie and SambarinoBCLS15
].
Theorem 10 ([
Reference GuichardGui, Reference SambarinoSam20
]). If
![]() $r \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
is the lift of a surface Hitchin representation and H is the Zariski closure of
$r \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
is the lift of a surface Hitchin representation and H is the Zariski closure of
![]() $r(\pi_1(S))$
, then:
$r(\pi_1(S))$
, then:
if
![]() $n=2k$
is even, H is conjugate to either
$n=2k$
is even, H is conjugate to either
![]() $\omega_n(SL(2,\mathbb{R}))$
,
$\omega_n(SL(2,\mathbb{R}))$
,
![]() $Sp(2k,\mathbb{R})$
or
$Sp(2k,\mathbb{R})$
or
![]() $SL(2k,\mathbb{R})$
;
$SL(2k,\mathbb{R})$
;
if
![]() $n=2k+1$
is odd and
$n=2k+1$
is odd and
![]() $n\neq7$
, then H is conjugate to either
$n\neq7$
, then H is conjugate to either
![]() $\omega_n(SL(2,\mathbb{R}))$
,
$\omega_n(SL(2,\mathbb{R}))$
,
![]() $SO(k,k+1)$
or
$SO(k,k+1)$
or
![]() $SL(2k+1,\mathbb{R})$
;
$SL(2k+1,\mathbb{R})$
;
if
![]() $n=7$
, then H is conjugate to either
$n=7$
, then H is conjugate to either
![]() $\omega_7(SL(2,\mathbb{R}))$
,
$\omega_7(SL(2,\mathbb{R}))$
,
![]() $G_2$
, SO(3,4) or
$G_2$
, SO(3,4) or
![]() $SL(7,\mathbb{R})$
.
$SL(7,\mathbb{R})$
.
3·2. A criterion for Zariski density
Here we prove Proposition 2 which gives us a criterion to find Zariski dense Hitchin representations.
Lemma 11. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
with n even be an orbifold Hitchin representation. Then for every
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
with n even be an orbifold Hitchin representation. Then for every
![]() $[\alpha] \in \pi_1({\mathcal{O}})$
of infinite order there is a lift
$[\alpha] \in \pi_1({\mathcal{O}})$
of infinite order there is a lift
![]() $A \in SL(n,\mathbb{R})$
of
$A \in SL(n,\mathbb{R})$
of
![]() $\rho([\alpha])$
which has n positive distinct eigenvalues.
$\rho([\alpha])$
which has n positive distinct eigenvalues.
Proof. First consider a Fuchsian representation
![]() $\sigma \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(2,\mathbb{R})$
and
$\sigma \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(2,\mathbb{R})$
and
![]() $[\alpha]$
an infinite order element of
$[\alpha]$
an infinite order element of
![]() $\pi_1({\mathcal{O}})$
. Since
$\pi_1({\mathcal{O}})$
. Since
![]() ${\mathcal{O}}$
is a hyperbolic orbifold,
${\mathcal{O}}$
is a hyperbolic orbifold,
![]() $\sigma([\alpha])$
is conjugate to a hyperbolic element
$\sigma([\alpha])$
is conjugate to a hyperbolic element
 $\begin{bmatrix} \lambda & 0 \\[5pt] 0 & \frac{1}{\lambda} \end{bmatrix} \in PSL(2,\mathbb{R})$
. We can lift this element to a matrix
$\begin{bmatrix} \lambda & 0 \\[5pt] 0 & \frac{1}{\lambda} \end{bmatrix} \in PSL(2,\mathbb{R})$
. We can lift this element to a matrix
 $\begin{pmatrix} \lambda & 0 \\[5pt] 0 & \frac{1}{\lambda} \end{pmatrix} \in SL(2,\mathbb{R})$
with
$\begin{pmatrix} \lambda & 0 \\[5pt] 0 & \frac{1}{\lambda} \end{pmatrix} \in SL(2,\mathbb{R})$
with
![]() $\lambda >0$
. Let
$\lambda >0$
. Let
![]() $\tilde\omega_n \;:\;\thinspace SL(2,\mathbb{R}) \to SL(n,\mathbb{R})$
be the unique irreducible representation in (1), then
$\tilde\omega_n \;:\;\thinspace SL(2,\mathbb{R}) \to SL(n,\mathbb{R})$
be the unique irreducible representation in (1), then
 $\tilde\omega_n\begin{pmatrix} \lambda & 0 \\[5pt] 0 & \frac{1}{\lambda} \end{pmatrix} \in SL(n,\mathbb{R})$
has n distinct positive eigenvalues
$\tilde\omega_n\begin{pmatrix} \lambda & 0 \\[5pt] 0 & \frac{1}{\lambda} \end{pmatrix} \in SL(n,\mathbb{R})$
has n distinct positive eigenvalues
![]() $\lambda^{n-1}, \lambda^{n-3}, \ldots, \lambda^{-(n-3)}, \lambda^{-(n-1)}$
and is a lift of
$\lambda^{n-1}, \lambda^{n-3}, \ldots, \lambda^{-(n-3)}, \lambda^{-(n-1)}$
and is a lift of
![]() $\omega_n\circ\sigma([\alpha])\in PSL(n,\mathbb{R})$
.
$\omega_n\circ\sigma([\alpha])\in PSL(n,\mathbb{R})$
.
Now consider a Hitchin representation
![]() $\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
. Let
$\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
. Let
![]() $\rho_t$
be a path of Hitchin representations such that
$\rho_t$
be a path of Hitchin representations such that
![]() $\rho_0$
is Fuchsian and
$\rho_0$
is Fuchsian and
![]() $\rho_1=\rho$
. This induces a path
$\rho_1=\rho$
. This induces a path
![]() $\rho_t([\alpha]) \subset PSL(n,\mathbb{R})$
. By the previous argument we may lift
$\rho_t([\alpha]) \subset PSL(n,\mathbb{R})$
. By the previous argument we may lift
![]() $\rho_t([\alpha])$
to a path
$\rho_t([\alpha])$
to a path
![]() $\tilde{A}_t \in SL(n,\mathbb{R})$
such that
$\tilde{A}_t \in SL(n,\mathbb{R})$
such that
![]() $\tilde{A}_0$
has n distinct positive eigenvalues. Since each eigenvalue of
$\tilde{A}_0$
has n distinct positive eigenvalues. Since each eigenvalue of
![]() $\tilde{A}_t$
varies continuously and
$\tilde{A}_t$
varies continuously and
![]() $\det\tilde{A}_t \neq 0$
, all eigenvalues of
$\det\tilde{A}_t \neq 0$
, all eigenvalues of
![]() $\tilde{A}_t$
are positive. Moreover, by Theorem 9 the absolute values of the eigenvalues of
$\tilde{A}_t$
are positive. Moreover, by Theorem 9 the absolute values of the eigenvalues of
![]() $\rho_t([\alpha])$
are distinct. This in turn implies all the eigenvalues of
$\rho_t([\alpha])$
are distinct. This in turn implies all the eigenvalues of
![]() $\tilde{A}_t$
are distinct. Therefore
$\tilde{A}_t$
are distinct. Therefore
![]() $\tilde{A}_1 \in SL(n,\mathbb{R})$
is a lift of
$\tilde{A}_1 \in SL(n,\mathbb{R})$
is a lift of
![]() $\rho([\alpha])$
with n positive distinct eigenvalues.
$\rho([\alpha])$
with n positive distinct eigenvalues.
To prove our criterion for Zariski density (Propositions 13 and 14) we will make use of the following theorem by Culver.
Theorem 12 ([
Reference CulverCul66
, theorem 2]). Let C be a real square matrix. Then the equation
![]() $C=\exp\!(X)$
has a unique real solution X if and only if all the eigenvalues of C are positive real and no elementary divisor (Jordan block) of C belonging to any eigenvalue appears more than once.
$C=\exp\!(X)$
has a unique real solution X if and only if all the eigenvalues of C are positive real and no elementary divisor (Jordan block) of C belonging to any eigenvalue appears more than once.
Proposition 13. Let
![]() $\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
with n even be an orbifold Hitchin representation so that
$\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
with n even be an orbifold Hitchin representation so that
![]() $\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
$\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
![]() $PSp(n,\mathbb{R})$
. If S is a surface finitely covering
$PSp(n,\mathbb{R})$
. If S is a surface finitely covering
![]() ${\mathcal{O}}$
then
${\mathcal{O}}$
then
![]() $\rho(\pi_1(S))$
is Zariski dense.
$\rho(\pi_1(S))$
is Zariski dense.
Proof. Let S be a surface finitely covering
![]() ${\mathcal{O}}$
and suppose that
${\mathcal{O}}$
and suppose that
![]() $\rho(\pi_1(S))$
is conjugate to a subgroup of
$\rho(\pi_1(S))$
is conjugate to a subgroup of
![]() $PSp(n,\mathbb{R})$
. Then there exists an alternating form
$PSp(n,\mathbb{R})$
. Then there exists an alternating form
![]() $\Omega\in SL(n,\mathbb{R})$
such that
$\Omega\in SL(n,\mathbb{R})$
such that
![]() $Sp(\Omega) = \{ g \in SL(n,\mathbb{R}) \ | \ g^T\Omega g = \Omega \}$
and
$Sp(\Omega) = \{ g \in SL(n,\mathbb{R}) \ | \ g^T\Omega g = \Omega \}$
and
![]() $\rho(\pi_1(S)) \subset PSp(\Omega) = Sp(\Omega)/\pm I$
.
$\rho(\pi_1(S)) \subset PSp(\Omega) = Sp(\Omega)/\pm I$
.
Let
![]() $[\alpha] \in \pi_1({\mathcal{O}})$
be an infinite order element. By Lemma 11 we can lift
$[\alpha] \in \pi_1({\mathcal{O}})$
be an infinite order element. By Lemma 11 we can lift
![]() $\rho([\alpha]) \in PSL(n,\mathbb{R})$
to a matrix
$\rho([\alpha]) \in PSL(n,\mathbb{R})$
to a matrix
![]() $A\in SL(n,\mathbb{R})$
with n positive distinct eigenvalues. Since
$A\in SL(n,\mathbb{R})$
with n positive distinct eigenvalues. Since
![]() $\pi_1(S)$
has finite index in
$\pi_1(S)$
has finite index in
![]() $\pi_1({\mathcal{O}})$
there exists a
$\pi_1({\mathcal{O}})$
there exists a
![]() $k\in \mathbb{N}$
such that
$k\in \mathbb{N}$
such that
![]() $\rho([\alpha])^k \in \rho(\pi_1(S))$
. Then
$\rho([\alpha])^k \in \rho(\pi_1(S))$
. Then
![]() $A^k$
is a lift of
$A^k$
is a lift of
![]() $\rho([\alpha])^k$
and
$\rho([\alpha])^k$
and
![]() $A^k \in Sp(\Omega)$
. Given that A has n positive distinct eigenvalues, by Theorem 12 there is a unique
$A^k \in Sp(\Omega)$
. Given that A has n positive distinct eigenvalues, by Theorem 12 there is a unique
![]() $X\in M_{n\times n}(\mathbb{R})$
such that
$X\in M_{n\times n}(\mathbb{R})$
such that
![]() $\exp\!(X) = A$
. Then using that
$\exp\!(X) = A$
. Then using that
![]() $\exp\!(kX) = A^k$
preserves
$\exp\!(kX) = A^k$
preserves
![]() $\Omega$
we get that
$\Omega$
we get that
 \begin{eqnarray*} \exp\!(kX)^T\Omega \exp\!(kX) = \Omega &\Longrightarrow& \Omega^{-1}\exp\!(kX)^T\Omega = \exp\!(kX)^{-1}\\[5pt] &\Longrightarrow& \exp\!(\Omega^{-1}(kX)^T\Omega) = \Omega^{-1}\exp\!(kX)^T\Omega =\exp\!(\!-kX).\end{eqnarray*}
\begin{eqnarray*} \exp\!(kX)^T\Omega \exp\!(kX) = \Omega &\Longrightarrow& \Omega^{-1}\exp\!(kX)^T\Omega = \exp\!(kX)^{-1}\\[5pt] &\Longrightarrow& \exp\!(\Omega^{-1}(kX)^T\Omega) = \Omega^{-1}\exp\!(kX)^T\Omega =\exp\!(\!-kX).\end{eqnarray*}
Applying Theorem 12 now to
![]() $\Omega^{-1}\exp\!(kX)^T\Omega$
we obtain that
$\Omega^{-1}\exp\!(kX)^T\Omega$
we obtain that
 \begin{eqnarray*} \Omega^{-1}(kX)^T\Omega = -kX &\Rightarrow& -\Omega(kX)^T\Omega = -kX\\[5pt] &\Rightarrow& \Omega(kX)^T\Omega = kX.\end{eqnarray*}
\begin{eqnarray*} \Omega^{-1}(kX)^T\Omega = -kX &\Rightarrow& -\Omega(kX)^T\Omega = -kX\\[5pt] &\Rightarrow& \Omega(kX)^T\Omega = kX.\end{eqnarray*}
This implies that
![]() $kX \in \mathfrak{sp}(\Omega)$
and thus
$kX \in \mathfrak{sp}(\Omega)$
and thus
![]() $A = \exp\!(X)\in Sp(\Omega)$
. Given that A is a lift of
$A = \exp\!(X)\in Sp(\Omega)$
. Given that A is a lift of
![]() $\rho([\alpha])$
, we have that
$\rho([\alpha])$
, we have that
![]() $\rho([\alpha]) \in PSp(\Omega)$
. Since
$\rho([\alpha]) \in PSp(\Omega)$
. Since
![]() $\pi_1({\mathcal{O}})$
is generated by its infinite order elements we get that
$\pi_1({\mathcal{O}})$
is generated by its infinite order elements we get that
![]() $\rho(\pi_1({\mathcal{O}})) \subset PSp(\Omega)$
, a contradiction. So it cannot be that
$\rho(\pi_1({\mathcal{O}})) \subset PSp(\Omega)$
, a contradiction. So it cannot be that
![]() $\rho(\pi_1(S))$
is conjugate to a subgroup of
$\rho(\pi_1(S))$
is conjugate to a subgroup of
![]() $PSp(n,\mathbb{R})$
. In particular, if r is a lift of the Hitchin surface representation
$PSp(n,\mathbb{R})$
. In particular, if r is a lift of the Hitchin surface representation
![]() $\rho|_{\pi_1(S)}$
then the Zariski closure of
$\rho|_{\pi_1(S)}$
then the Zariski closure of
![]() $r(\pi_1(S))$
cannot be conjugate to a subgroup of
$r(\pi_1(S))$
cannot be conjugate to a subgroup of
![]() $Sp(n,\mathbb{R})$
. By Theorem 10 it must be that the Zariski closure of
$Sp(n,\mathbb{R})$
. By Theorem 10 it must be that the Zariski closure of
![]() $r(\pi_1(S))$
is
$r(\pi_1(S))$
is
![]() $SL(n,\mathbb{R})$
. Therefore the Zariski closure of
$SL(n,\mathbb{R})$
. Therefore the Zariski closure of
![]() $\rho(\pi_1(S))$
is
$\rho(\pi_1(S))$
is
![]() $PSL(n,\mathbb{R})$
.
$PSL(n,\mathbb{R})$
.
In the case when
![]() $n=2k+1$
is odd, by Theorem 10 the Zariski closure of
$n=2k+1$
is odd, by Theorem 10 the Zariski closure of
![]() $\rho(\pi_1(S))$
where
$\rho(\pi_1(S))$
where
![]() $\rho$
is a surface Hitchin representation is either conjugate to a subgroup of
$\rho$
is a surface Hitchin representation is either conjugate to a subgroup of
![]() $SO(k,k+1)$
or equals
$SO(k,k+1)$
or equals
![]() $SL(n,\mathbb{R})$
. By assuming there exists a symmetric bilinear form J such that
$SL(n,\mathbb{R})$
. By assuming there exists a symmetric bilinear form J such that
![]() $\rho(\pi_1(S)) \subset SO(J)$
we have an analogous proof to that of Proposition 13 to get a criterion for Zariski density of surface Hitchin representations in the odd case.
$\rho(\pi_1(S)) \subset SO(J)$
we have an analogous proof to that of Proposition 13 to get a criterion for Zariski density of surface Hitchin representations in the odd case.
Proposition 14. Let
![]() $\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
with n odd be an orbifold Hitchin representation such that there is no real quadratic form J for which
$\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
with n odd be an orbifold Hitchin representation such that there is no real quadratic form J for which
![]() $\rho(\pi_1({\mathcal{O}}))\subset SO(J)$
. If S is a surface finitely covering
$\rho(\pi_1({\mathcal{O}}))\subset SO(J)$
. If S is a surface finitely covering
![]() ${\mathcal{O}}$
then
${\mathcal{O}}$
then
![]() $\rho(\pi_1(S))$
is Zariski dense.
$\rho(\pi_1(S))$
is Zariski dense.
Given that any finite index subgroup of
![]() $\pi_1({\mathcal{O}})$
contains a surface subgroup which has finite index in
$\pi_1({\mathcal{O}})$
contains a surface subgroup which has finite index in
![]() $\pi_1({\mathcal{O}})$
we obtain the following result.
$\pi_1({\mathcal{O}})$
we obtain the following result.
Proposition 15. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
be an orbifold Hitchin representation such that:
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to PSL(n,\mathbb{R})$
be an orbifold Hitchin representation such that:
if
![]() $n=2k$
is even then
$n=2k$
is even then
![]() $\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
$\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
![]() $PSp(2k,\mathbb{R})$
or,
$PSp(2k,\mathbb{R})$
or,
if
![]() $n=2k+1$
is odd then
$n=2k+1$
is odd then
![]() $\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
$\rho(\pi_1({\mathcal{O}}))$
is not conjugate to a subgroup of
![]() $PSO(k,k+1)$
.
$PSO(k,k+1)$
.
Then for every finite index subgroup H of
![]() $\pi_1({\mathcal{O}})$
the image
$\pi_1({\mathcal{O}})$
the image
![]() $\rho(H)$
is Zariski dense in
$\rho(H)$
is Zariski dense in
![]() $PSL(n,\mathbb{R})$
.
$PSL(n,\mathbb{R})$
.
4. Bending representations of orbifold groups
Theorem 19 in this section gives a general construction of a path
![]() $\rho_t$
of Zariski dense Hitchin surface representations into
$\rho_t$
of Zariski dense Hitchin surface representations into
![]() $SL(n,\mathbb{R})$
for odd n. By requiring that the initial representation
$SL(n,\mathbb{R})$
for odd n. By requiring that the initial representation
![]() $\rho_0$
has image inside
$\rho_0$
has image inside
![]() $SL(n,\mathbb{Q})$
we obtain Corollary 20, in which every representation
$SL(n,\mathbb{Q})$
we obtain Corollary 20, in which every representation
![]() $\rho_t$
with
$\rho_t$
with
![]() $t\in \mathbb{Q}$
also has image in
$t\in \mathbb{Q}$
also has image in
![]() $SL(n,\mathbb{Q})$
.
$SL(n,\mathbb{Q})$
.
4·1. Bending representations
Let
![]() ${\mathcal{O}}$
be a 2-dimensional orientable connected closed orbifold of negative orbifold Euler characteristic and
${\mathcal{O}}$
be a 2-dimensional orientable connected closed orbifold of negative orbifold Euler characteristic and
![]() ${\mathcal{O}}_L$
,
${\mathcal{O}}_L$
,
![]() ${\mathcal{O}}_R$
be open connected suborbifolds with connected intersection
${\mathcal{O}}_R$
be open connected suborbifolds with connected intersection
![]() ${\mathcal{O}}_L\cap {\mathcal{O}}_R$
. Given a representation
${\mathcal{O}}_L\cap {\mathcal{O}}_R$
. Given a representation
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to G$
there is a standard way of “bending”
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to G$
there is a standard way of “bending”
![]() $\rho$
by an element
$\rho$
by an element
![]() $\delta$
of the centraliser in G of
$\delta$
of the centraliser in G of
![]() $\rho(\pi_1({\mathcal{O}}_L\cap {\mathcal{O}}_R))$
to obtain a representation
$\rho(\pi_1({\mathcal{O}}_L\cap {\mathcal{O}}_R))$
to obtain a representation
![]() $\rho_\delta \;:\;\thinspace \pi_1({\mathcal{O}}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\pi_1({\mathcal{O}}_L\cap{\mathcal{O}}_R)}\pi_1({\mathcal{O}}_R)\to G$
so that
$\rho_\delta \;:\;\thinspace \pi_1({\mathcal{O}}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\pi_1({\mathcal{O}}_L\cap{\mathcal{O}}_R)}\pi_1({\mathcal{O}}_R)\to G$
so that
![]() $\rho_\delta(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)), \delta \rho(\pi_1({\mathcal{O}}_R))\delta^{-1}\rangle$
(see for example [
Reference GoldmanGol87
, section 5].
$\rho_\delta(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)), \delta \rho(\pi_1({\mathcal{O}}_R))\delta^{-1}\rangle$
(see for example [
Reference GoldmanGol87
, section 5].
From now onwards we will consider the case where there is a simple closed curve
![]() $\gamma \subset {\mathcal{O}}$
, not parallel to a cone point, that divides
$\gamma \subset {\mathcal{O}}$
, not parallel to a cone point, that divides
![]() ${\mathcal{O}}$
into two orbifolds
${\mathcal{O}}$
into two orbifolds
![]() ${\mathcal{O}}_L$
and
${\mathcal{O}}_L$
and
![]() ${\mathcal{O}}_R$
which share
${\mathcal{O}}_R$
which share
![]() $\gamma$
as their common boundary, so that
$\gamma$
as their common boundary, so that
![]() $\pi_1({\mathcal{O}}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R).$
$\pi_1({\mathcal{O}}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R).$
Proposition 16. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}})\simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R) \to SL(n,\mathbb{Q})$
be a representation for which
$\rho \;:\;\thinspace \pi_1({\mathcal{O}})\simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R) \to SL(n,\mathbb{Q})$
be a representation for which
![]() $\rho([\gamma])$
has n distinct positive eigenvalues. Then there exists a path of representations
$\rho([\gamma])$
has n distinct positive eigenvalues. Then there exists a path of representations
![]() $\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
with
$\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
with
![]() $t\geq0$
such that:
$t\geq0$
such that:
-
(i)
 $\rho_0 = \rho$
;
$\rho_0 = \rho$
; -
(ii)
 $\rho_t(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)),\delta_t \rho(\pi_1({\mathcal{O}}_R)) \delta_t^{-1}\rangle$
for some
$\rho_t(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)),\delta_t \rho(\pi_1({\mathcal{O}}_R)) \delta_t^{-1}\rangle$
for some
 $\delta_t\in SL(n,\mathbb{R})$
which commutes with
$\delta_t\in SL(n,\mathbb{R})$
which commutes with
 $\rho([\gamma])$
; and
$\rho([\gamma])$
; and -
(iii)
 $\rho_t$
has image in
$\rho_t$
has image in
 $SL(n,\mathbb{Q})$
for every
$SL(n,\mathbb{Q})$
for every
 $t\in \mathbb{Q}$
.
$t\in \mathbb{Q}$
.
Proof. The matrix
![]() $\rho([\gamma])$
is conjugate to a diagonal matrix D with entries
$\rho([\gamma])$
is conjugate to a diagonal matrix D with entries
![]() $\lambda_1, \ldots, \lambda_n >0$
along its diagonal. Now for every
$\lambda_1, \ldots, \lambda_n >0$
along its diagonal. Now for every
![]() $t>0$
define
$t>0$
define
Notice that
![]() $\det(t\rho([\gamma]) + I) = \det(tD + I) = \Pi_{k=1}^{n}(t\lambda_i +1)>0$
, so
$\det(t\rho([\gamma]) + I) = \det(tD + I) = \Pi_{k=1}^{n}(t\lambda_i +1)>0$
, so
![]() $t\rho([\gamma]) +I$
is invertible for all t. Then each
$t\rho([\gamma]) +I$
is invertible for all t. Then each
![]() $\delta_t$
is in
$\delta_t$
is in
![]() $SL(n,\mathbb{R})$
and we can check that
$SL(n,\mathbb{R})$
and we can check that
![]() $\delta_t$
commutes with
$\delta_t$
commutes with
![]() $\rho([\gamma])$
. Since
$\rho([\gamma])$
. Since
![]() $\rho$
is a rational representation, whenever
$\rho$
is a rational representation, whenever
![]() $t\in \mathbb{Q}$
the matrix
$t\in \mathbb{Q}$
the matrix
![]() $t\rho([\gamma]) + I$
has rational entries and non-zero determinant.
$t\rho([\gamma]) + I$
has rational entries and non-zero determinant.
Let
![]() $\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
be the representation such that
$\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
be the representation such that
![]() $\rho_t(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)),\delta_t \rho(\pi_1({\mathcal{O}}_R)) \delta_t^{-1}\rangle$
. Notice that
$\rho_t(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)),\delta_t \rho(\pi_1({\mathcal{O}}_R)) \delta_t^{-1}\rangle$
. Notice that
![]() $\rho_0 = \rho$
and that for every
$\rho_0 = \rho$
and that for every
![]() $t\in\mathbb{Q}$
the representation
$t\in\mathbb{Q}$
the representation
![]() $\rho_t$
has image in
$\rho_t$
has image in
![]() $SL(n,\mathbb{Q})$
.
$SL(n,\mathbb{Q})$
.
4·2. Discarding Zariski closures
For the rest of Section 4 we focus on the case where
![]() $n=2k+1$
is odd. Recall that in this case
$n=2k+1$
is odd. Recall that in this case
![]() $SL(n,\mathbb{R}) \equiv PSL(n,\mathbb{R})$
.
$SL(n,\mathbb{R}) \equiv PSL(n,\mathbb{R})$
.
Lemma 17. Let
![]() $\rho\;:\;\thinspace\Gamma \to SL(n,\mathbb{R})$
be an irreducible representation and suppose there is a quadratic form J such that
$\rho\;:\;\thinspace\Gamma \to SL(n,\mathbb{R})$
be an irreducible representation and suppose there is a quadratic form J such that
![]() $\rho(\Gamma )\subset SO(J)$
. Then J is unique up to scaling.
$\rho(\Gamma )\subset SO(J)$
. Then J is unique up to scaling.
Proof. Suppose
![]() $\rho(\Gamma)< SO(J_1)\cap SO(J_2)$
. Then for any
$\rho(\Gamma)< SO(J_1)\cap SO(J_2)$
. Then for any
![]() $\rho(\gamma) \in \rho(\Gamma)$
we have that
$\rho(\gamma) \in \rho(\Gamma)$
we have that
which implies that
![]() $\rho(\gamma)J_1J_2^{-1} = J_1J_2^{-1}\rho(\gamma).$
Since n is odd,
$\rho(\gamma)J_1J_2^{-1} = J_1J_2^{-1}\rho(\gamma).$
Since n is odd,
![]() $J_1J_2^{-1}$
has a real eigenvalue
$J_1J_2^{-1}$
has a real eigenvalue
![]() $\lambda$
. Then
$\lambda$
. Then
![]() $\text{Ker} (J_1J_2^{-1} - \lambda I)$
is a non-zero invariant subspace for the irreducible representation
$\text{Ker} (J_1J_2^{-1} - \lambda I)$
is a non-zero invariant subspace for the irreducible representation
![]() $\rho$
, which implies
$\rho$
, which implies
![]() $J_1 = \lambda J_2$
.
$J_1 = \lambda J_2$
.
Proposition 18. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}})\simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R) \to SL(n,\mathbb{R})$
be a representation in which the restrictions
$\rho \;:\;\thinspace \pi_1({\mathcal{O}})\simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R) \to SL(n,\mathbb{R})$
be a representation in which the restrictions
![]() $\rho|_{\pi_1({\mathcal{O}}_L)}$
and
$\rho|_{\pi_1({\mathcal{O}}_L)}$
and
![]() $\rho|_{\pi_1({\mathcal{O}}_R)}$
are irreducible and
$\rho|_{\pi_1({\mathcal{O}}_R)}$
are irreducible and
![]() $\rho([\gamma])$
has n positive distinct eigenvalues. Suppose there is a quadratic form J such that
$\rho([\gamma])$
has n positive distinct eigenvalues. Suppose there is a quadratic form J such that
![]() $\rho(\pi_1({\mathcal{O}}))\subset SO(J)$
. Then there exists a path of representations
$\rho(\pi_1({\mathcal{O}}))\subset SO(J)$
. Then there exists a path of representations
![]() $\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
such that:
$\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
such that:
-
(i)
 $\rho_0 = \rho$
and
$\rho_0 = \rho$
and -
(ii) for each
 $t>0$
there is no quadratic form
$t>0$
there is no quadratic form
 $\tilde{J}$
such that
$\tilde{J}$
such that
 $\rho_t(\pi_1({\mathcal{O}}))\subset SO(\tilde{J})$
.
$\rho_t(\pi_1({\mathcal{O}}))\subset SO(\tilde{J})$
.
Proof. By Proposition 16 there are
![]() $\delta_t\in SL(n,\mathbb{R})$
that commute with
$\delta_t\in SL(n,\mathbb{R})$
that commute with
![]() $\rho([\gamma])$
, with which we can construct a path of representations
$\rho([\gamma])$
, with which we can construct a path of representations
![]() $\rho_t\;:\;\thinspace \pi_1({\mathcal{O}})\to SL(n,\mathbb{R})$
such that
$\rho_t\;:\;\thinspace \pi_1({\mathcal{O}})\to SL(n,\mathbb{R})$
such that
![]() $\rho_0=\rho$
and
$\rho_0=\rho$
and
![]() $\rho_t(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)),\delta_t \rho(\pi_1({\mathcal{O}}_R)) \delta_t^{-1}\rangle$
.
$\rho_t(\pi_1({\mathcal{O}})) = \langle \rho(\pi_1({\mathcal{O}}_L)),\delta_t \rho(\pi_1({\mathcal{O}}_R)) \delta_t^{-1}\rangle$
.
Now fix
![]() $t>0$
. Suppose there exists a quadratic form
$t>0$
. Suppose there exists a quadratic form
![]() $\tilde{J}$
such that
$\tilde{J}$
such that
![]() $\rho_t(\pi_1({\mathcal{O}})) \subset SO(\tilde{J})$
. Since
$\rho_t(\pi_1({\mathcal{O}})) \subset SO(\tilde{J})$
. Since
![]() $\rho(\pi_1({\mathcal{O}})) \subset SO(J)$
, in particular
$\rho(\pi_1({\mathcal{O}})) \subset SO(J)$
, in particular
![]() $\rho_t(\pi_1({\mathcal{O}}_L)) = \rho_0(\pi_1({\mathcal{O}}_L)) \subset SO(J)\cap SO(\tilde{J})$
. The restriction
$\rho_t(\pi_1({\mathcal{O}}_L)) = \rho_0(\pi_1({\mathcal{O}}_L)) \subset SO(J)\cap SO(\tilde{J})$
. The restriction
![]() $\rho_t|_{\pi_1({\mathcal{O}}_L)}$
is irreducible, so by Lemma 17 J is a real multiple of
$\rho_t|_{\pi_1({\mathcal{O}}_L)}$
is irreducible, so by Lemma 17 J is a real multiple of
![]() $\tilde{J}$
. Similarly, by construction
$\tilde{J}$
. Similarly, by construction
![]() $\rho_t (\pi_1({\mathcal{O}}_R)) \subset SO(\delta_t J \delta_t^T)\cap SO(\tilde{J})$
and
$\rho_t (\pi_1({\mathcal{O}}_R)) \subset SO(\delta_t J \delta_t^T)\cap SO(\tilde{J})$
and
![]() $\rho_t|_{\pi_1({\mathcal{O}}_R)}$
is irreducible too. Thus
$\rho_t|_{\pi_1({\mathcal{O}}_R)}$
is irreducible too. Thus
![]() $\delta_t J \delta_t^T$
is also a multiple of
$\delta_t J \delta_t^T$
is also a multiple of
![]() $\tilde{J}$
. This implies there is a
$\tilde{J}$
. This implies there is a
![]() $\lambda \in \mathbb{R}$
such that
$\lambda \in \mathbb{R}$
such that
![]() $\lambda J = \delta_t J \delta_t^T$
and then
$\lambda J = \delta_t J \delta_t^T$
and then
![]() $\lambda^n = \det(\delta_t)^2 =1.$
Since n is odd it must be that
$\lambda^n = \det(\delta_t)^2 =1.$
Since n is odd it must be that
![]() $\lambda =1 $
and we obtain
$\lambda =1 $
and we obtain
![]() $\delta_t \in SO(J)$
. Given that
$\delta_t \in SO(J)$
. Given that
having
![]() $J = \delta_tJ\delta_t^T$
would imply that
$J = \delta_tJ\delta_t^T$
would imply that
![]() $ \mu I = \rho([\gamma])^{-1} + \rho([\gamma])$
for some
$ \mu I = \rho([\gamma])^{-1} + \rho([\gamma])$
for some
![]() $\mu\in \mathbb{R}$
. Recall that
$\mu\in \mathbb{R}$
. Recall that
![]() $\rho([\gamma])$
is conjugate to a diagonal matrix D whose eigenvalues are all distinct. If
$\rho([\gamma])$
is conjugate to a diagonal matrix D whose eigenvalues are all distinct. If
![]() $\mu I = \rho([\gamma])^{-1} + \rho([\gamma])$
then by conjugating we would obtain that
$\mu I = \rho([\gamma])^{-1} + \rho([\gamma])$
then by conjugating we would obtain that
![]() $\mu I = D^{-1} + D$
, which is not the case given that
$\mu I = D^{-1} + D$
, which is not the case given that
![]() $n>2$
.
$n>2$
.
4·3. Representations of surface groups
Recall we are assuming that
![]() ${\mathcal{O}}$
is a 2-dimensional orientable connected closed orbifold of negative orbifold Euler characteristic. Such orbifolds are always finitely covered by a surface S of genus greater than one, so
${\mathcal{O}}$
is a 2-dimensional orientable connected closed orbifold of negative orbifold Euler characteristic. Such orbifolds are always finitely covered by a surface S of genus greater than one, so
![]() $\pi_1(S)$
is a finite index subgroup of
$\pi_1(S)$
is a finite index subgroup of
![]() $\pi_1({\mathcal{O}})$
. Given a representation
$\pi_1({\mathcal{O}})$
. Given a representation
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to G$
we will denote the restriction of
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to G$
we will denote the restriction of
![]() $\rho$
to
$\rho$
to
![]() $\pi_1(S)$
by
$\pi_1(S)$
by
![]() $\rho^S$
.
$\rho^S$
.
Theorem 19. Suppose
![]() $\pi_1({\mathcal{O}})\simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R)$
with
$\pi_1({\mathcal{O}})\simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R)$
with
![]() $[\gamma]$
an infinite order element. Let
$[\gamma]$
an infinite order element. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
be an orbifold Fuchsian representation such that the restrictions
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
be an orbifold Fuchsian representation such that the restrictions
![]() $\rho|_{\pi_1({\mathcal{O}}_L)}$
and
$\rho|_{\pi_1({\mathcal{O}}_L)}$
and
![]() $\rho|_{\pi_1({\mathcal{O}}_R)}$
are irreducible. If S is a surface finitely covering
$\rho|_{\pi_1({\mathcal{O}}_R)}$
are irreducible. If S is a surface finitely covering
![]() ${\mathcal{O}}$
then there exists a path of representations
${\mathcal{O}}$
then there exists a path of representations
![]() $\rho^S_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
such that
$\rho^S_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
such that
![]() $\rho^S_0 = \rho^S$
and
$\rho^S_0 = \rho^S$
and
![]() $\rho_t^S$
is a Zariski dense surface Hitchin representation for each
$\rho_t^S$
is a Zariski dense surface Hitchin representation for each
![]() $t>0$
.
$t>0$
.
Proof. Since
![]() $\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
is an orbifold Hitchin representation with odd
$\rho\;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
is an orbifold Hitchin representation with odd
![]() $n=2k+1$
and
$n=2k+1$
and
![]() $[\gamma]$
has infinite order, then
$[\gamma]$
has infinite order, then
![]() $\rho([\gamma])$
has n positive distinct real eigenvalues. Moreover, since
$\rho([\gamma])$
has n positive distinct real eigenvalues. Moreover, since
![]() $\rho$
is Fuchsian its image is contained in a conjugate of
$\rho$
is Fuchsian its image is contained in a conjugate of
![]() $SO(k,k+1)$
. Using Proposition 18 we obtain a path of representations
$SO(k,k+1)$
. Using Proposition 18 we obtain a path of representations
![]() $\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
such that
$\rho_t \;:\;\thinspace \pi_1({\mathcal{O}}) \to SL(n,\mathbb{R})$
such that
![]() $\rho_0 = \rho$
and for each
$\rho_0 = \rho$
and for each
![]() $t>0$
there is no real quadratic form J such that
$t>0$
there is no real quadratic form J such that
![]() $\rho_t(\pi_1({\mathcal{O}}))\subset SO(J)$
. By Proposition 14 each
$\rho_t(\pi_1({\mathcal{O}}))\subset SO(J)$
. By Proposition 14 each
![]() $\rho_t(\pi_1(S))$
is Zariski dense in
$\rho_t(\pi_1(S))$
is Zariski dense in
![]() $SL(n,\mathbb{R})$
.
$SL(n,\mathbb{R})$
.
Now consider the continuous path
![]() $[\rho_t] \in \text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
for
$[\rho_t] \in \text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
for
![]() $t\geq0$
. Its image is connected so all
$t\geq0$
. Its image is connected so all
![]() $PGL(n,\mathbb{R})$
-conjugacy classes
$PGL(n,\mathbb{R})$
-conjugacy classes
![]() $[\rho_t]$
are contained in the same connected component of
$[\rho_t]$
are contained in the same connected component of
![]() $\text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
. Because the representation
$\text{Rep}(\pi_1({\mathcal{O}}),PGL(n,\mathbb{R}))$
. Because the representation
![]() $\rho_0 = \rho$
is Fuchsian,
$\rho_0 = \rho$
is Fuchsian,
![]() $[\rho_0]$
is in the Hitchin component
$[\rho_0]$
is in the Hitchin component
![]() $\text{Hit}(\pi_1({\mathcal{O}}), PGL(n,\mathbb{R}))$
and so is every
$\text{Hit}(\pi_1({\mathcal{O}}), PGL(n,\mathbb{R}))$
and so is every
![]() $[\rho_t]$
. Thus, by Theorem 9, each
$[\rho_t]$
. Thus, by Theorem 9, each
![]() $\rho_t$
is discrete, faithful and strongly irreducible. Since
$\rho_t$
is discrete, faithful and strongly irreducible. Since
![]() $\pi_1(S)$
has finite index in
$\pi_1(S)$
has finite index in
![]() $\pi_1({\mathcal{O}})$
, each restriction
$\pi_1({\mathcal{O}})$
, each restriction
![]() $\rho^S_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
is irreducible. In particular
$\rho^S_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
is irreducible. In particular
![]() $\rho_0^S$
is a surface Fuchsian representation. Then
$\rho_0^S$
is a surface Fuchsian representation. Then
![]() $[\rho^S_t]$
is a continuous path in
$[\rho^S_t]$
is a continuous path in
![]() $\text{Rep}^+(\pi_1(S),SL(n,\mathbb{R}))$
with
$\text{Rep}^+(\pi_1(S),SL(n,\mathbb{R}))$
with
![]() $[\rho_0^S] \in \text{Hit}(\pi_1(S),SL(n,\mathbb{R}))$
. Since the Hitchin component is path connected
$[\rho_0^S] \in \text{Hit}(\pi_1(S),SL(n,\mathbb{R}))$
. Since the Hitchin component is path connected
![]() $[\rho^S_t] \in \text{Hit}(\pi_1(S),SL(n,\mathbb{R}))$
for all
$[\rho^S_t] \in \text{Hit}(\pi_1(S),SL(n,\mathbb{R}))$
for all
![]() $t\geq0$
.
$t\geq0$
.
To finish this section notice that the construction of the path of Zariski dense representations in the previous theorem is based on Proposition 16, so we may add the assumption of
![]() $\rho(\pi_1({\mathcal{O}}))\subset SL(n,\mathbb{Q})$
to obtain that the image of every
$\rho(\pi_1({\mathcal{O}}))\subset SL(n,\mathbb{Q})$
to obtain that the image of every
![]() $\rho_t$
is in
$\rho_t$
is in
![]() $SL(n,\mathbb{Q})$
for every
$SL(n,\mathbb{Q})$
for every
![]() $t\in \mathbb{Q}$
.
$t\in \mathbb{Q}$
.
Corollary 20. Let
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}})\to PSL(n,\mathbb{Q})$
be a representation satisfying the assumptions of Theorem 19. If S is a surface finitely covering
$\rho \;:\;\thinspace \pi_1({\mathcal{O}})\to PSL(n,\mathbb{Q})$
be a representation satisfying the assumptions of Theorem 19. If S is a surface finitely covering
![]() ${\mathcal{O}}$
then there exists a path
${\mathcal{O}}$
then there exists a path
![]() $\rho^S_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
of Hitchin representations such that
$\rho^S_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
of Hitchin representations such that
![]() $\rho^S_0 = \rho^S$
,
$\rho^S_0 = \rho^S$
,
![]() $\rho_t^S$
is Zariski dense for each
$\rho_t^S$
is Zariski dense for each
![]() $t>0$
and
$t>0$
and
![]() $\rho_t^S$
has image in
$\rho_t^S$
has image in
![]() $SL(n,\mathbb{Q})$
for every
$SL(n,\mathbb{Q})$
for every
![]() $t\in \mathbb{Q}$
.
$t\in \mathbb{Q}$
.
5. Representations of
 $\pi_1({\mathcal{O}}_{3,3,3,3})$
$\pi_1({\mathcal{O}}_{3,3,3,3})$
In this section we look at the orbifold
![]() ${\mathcal{O}}_{3,3,3,3}$
and find a Fuchsian representation
${\mathcal{O}}_{3,3,3,3}$
and find a Fuchsian representation
![]() $\rho \;:\;\thinspace \pi_1({\mathcal{O}}_{3,3,3,3})\to SL(n,\mathbb{Z})$
satisfying the assumptions of Corollary 20.
$\rho \;:\;\thinspace \pi_1({\mathcal{O}}_{3,3,3,3})\to SL(n,\mathbb{Z})$
satisfying the assumptions of Corollary 20.
5·1. The orbifold
 ${\mathcal{O}}_{3,3,3,3}$
${\mathcal{O}}_{3,3,3,3}$
In what follows we focus on the triangle group
![]() $\Delta(3,4,4) \subset PSL(2,\mathbb{R})$
. If we let T be the hyperbolic triangle with angles
$\Delta(3,4,4) \subset PSL(2,\mathbb{R})$
. If we let T be the hyperbolic triangle with angles
![]() $\{{\pi}/{3}$
,
$\{{\pi}/{3}$
,
![]() ${\pi}/{4}$
,
${\pi}/{4}$
,
![]() ${\pi}/{4}\}$
, then the generators of
${\pi}/{4}\}$
, then the generators of
![]() $\Delta(3,4,4)$
are the rotations x and y by
$\Delta(3,4,4)$
are the rotations x and y by
![]() ${2\pi}/{3}$
and
${2\pi}/{3}$
and
![]() ${\pi}/{2}$
around the corresponding vertices of T. This group has presentation
${\pi}/{2}$
around the corresponding vertices of T. This group has presentation
The fundamental domain for the action of
![]() $\Delta(3,4,4)$
on
$\Delta(3,4,4)$
on
![]() $\mathbb{H}^{2} $
is a quadrilateral with angles
$\mathbb{H}^{2} $
is a quadrilateral with angles
![]() $\{{\pi}/{2},{\pi}/{3},{\pi}/{2},{\pi}/{3}\}$
. The quotient
$\{{\pi}/{2},{\pi}/{3},{\pi}/{2},{\pi}/{3}\}$
. The quotient
![]() $\mathbb{H}^{2} /\Delta(3,4,4)$
is homeomorphic to the orbifold
$\mathbb{H}^{2} /\Delta(3,4,4)$
is homeomorphic to the orbifold
![]() $S^2(3,4,4)$
whose underlying topological space is
$S^2(3,4,4)$
whose underlying topological space is
![]() $S^2$
and has three cone points of orders
$S^2$
and has three cone points of orders
![]() $3,\ 4$
and 4 (Figure 1). This defines, up to conjugation, an isomorphism
$3,\ 4$
and 4 (Figure 1). This defines, up to conjugation, an isomorphism
![]() $\pi_1(S^2(3,4,4))\to \Delta(3,4,4)\subset PSL(2,\mathbb{R})$
.
$\pi_1(S^2(3,4,4))\to \Delta(3,4,4)\subset PSL(2,\mathbb{R})$
.

Fig. 1. Orbifold
![]() $S^2(3,4,4)$
.
$S^2(3,4,4)$
.
Let
![]() $\theta_1 = x $
and
$\theta_1 = x $
and
![]() $ \theta_i = y\theta_{i-1}y^{-1} $
for
$ \theta_i = y\theta_{i-1}y^{-1} $
for
![]() $ i = 2,3,4$
, then
$ i = 2,3,4$
, then
![]() $\langle \theta_1, \ldots, \theta_4 \rangle$
the quotient of
$\langle \theta_1, \ldots, \theta_4 \rangle$
the quotient of
![]() $\mathbb{H}^{2} $
by the action of
$\mathbb{H}^{2} $
by the action of
![]() $\langle \theta_1, \ldots, \theta_4 \rangle$
is homeomorphic to the orbifold
$\langle \theta_1, \ldots, \theta_4 \rangle$
is homeomorphic to the orbifold
![]() $\mathcal{O}_{3,3,3,3}$
with underlying topological space
$\mathcal{O}_{3,3,3,3}$
with underlying topological space
![]() $S^2$
and 4 cone points of order 3. By construction, we obtain that
$S^2$
and 4 cone points of order 3. By construction, we obtain that
![]() $\mathcal{O}_{3,3,3,3}$
is an index four orbifold covering of
$\mathcal{O}_{3,3,3,3}$
is an index four orbifold covering of
![]() $S^2(3,4,4)$
. If
$S^2(3,4,4)$
. If
![]() $ \gamma_1, \ldots, \gamma_4$
are loops around the cone points of
$ \gamma_1, \ldots, \gamma_4$
are loops around the cone points of
![]() $\mathcal{O}_{3,3,3,3}$
, then the orbifold fundamental group has the presentation
$\mathcal{O}_{3,3,3,3}$
, then the orbifold fundamental group has the presentation
Identifying each
![]() $ \gamma_i$
with the rotation
$ \gamma_i$
with the rotation
![]() $\theta_i$
gives an isomorphism
$\theta_i$
gives an isomorphism
![]() $\pi_1(\mathcal{O}_{3,3,3,3})\cong \langle \theta_1, \ldots, \theta_4\rangle$
which defines (up to conjugation) a discrete and faithful representation
$\pi_1(\mathcal{O}_{3,3,3,3})\cong \langle \theta_1, \ldots, \theta_4\rangle$
which defines (up to conjugation) a discrete and faithful representation
It follows from the Borel density theorem that
![]() $\sigma$
is a Zariski dense representation.
$\sigma$
is a Zariski dense representation.
5·2. Rational representations of
 $\pi_1({\mathcal{O}}_{3,3,3,3})$
$\pi_1({\mathcal{O}}_{3,3,3,3})$
We will now focus on the case
![]() $n=2k+1$
and the representation
$n=2k+1$
and the representation
![]() $ \omega_n \circ \sigma \;:\;\thinspace \pi_1(\mathcal{O}_{3,3,3,3}) \to SL(n,\mathbb{R}),$
where
$ \omega_n \circ \sigma \;:\;\thinspace \pi_1(\mathcal{O}_{3,3,3,3}) \to SL(n,\mathbb{R}),$
where
![]() $\sigma$
is the representation defined in (4) and
$\sigma$
is the representation defined in (4) and
![]() $\omega_n\;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R}) =SL(n,\mathbb{R})$
the irreducible representation introduced in Section 3·1. Since
$\omega_n\;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R}) =SL(n,\mathbb{R})$
the irreducible representation introduced in Section 3·1. Since
![]() $\omega_n\circ \sigma$
is an orbifold Fuchsian representation, it is irreducible. The following result implies that we can conjugate
$\omega_n\circ \sigma$
is an orbifold Fuchsian representation, it is irreducible. The following result implies that we can conjugate
![]() $\omega_n\circ \sigma$
to obtain an integral representation
$\omega_n\circ \sigma$
to obtain an integral representation
Proposition 21 ([
Reference Long and ThistlethwaiteLT20
, theorem 2·1]). Let
![]() $\omega_n\;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
be the unique irreducible representation between these groups. Then for every odd n the restriction
$\omega_n\;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
be the unique irreducible representation between these groups. Then for every odd n the restriction
![]() $\phi_n = \omega_n |_{\Delta(3,4,4)}$
is conjugate to a representation
$\phi_n = \omega_n |_{\Delta(3,4,4)}$
is conjugate to a representation
![]() $\rho_n \;:\;\thinspace \Delta(3,4,4) \to PSL(n,\mathbb{Z})$
.
$\rho_n \;:\;\thinspace \Delta(3,4,4) \to PSL(n,\mathbb{Z})$
.
Now let
![]() $\gamma \subset {\mathcal{O}}_{3,3,3,3}$
be a simple closed loop dividing
$\gamma \subset {\mathcal{O}}_{3,3,3,3}$
be a simple closed loop dividing
![]() ${\mathcal{O}}_{3,3,3,3}$
into two orbifolds
${\mathcal{O}}_{3,3,3,3}$
into two orbifolds
![]() ${\mathcal{O}}_L$
and
${\mathcal{O}}_L$
and
![]() ${\mathcal{O}}_R$
which share
${\mathcal{O}}_R$
which share
![]() $\gamma$
as their common boundary and have two cone points of order 3 each. Then
$\gamma$
as their common boundary and have two cone points of order 3 each. Then
![]() $[\gamma] \in \pi_1({\mathcal{O}}_{3,3,3,3})$
is an infinite order element and
$[\gamma] \in \pi_1({\mathcal{O}}_{3,3,3,3})$
is an infinite order element and
![]() $\pi_1({\mathcal{O}}_{3,3,3,3}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R).$
$\pi_1({\mathcal{O}}_{3,3,3,3}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R).$
Proposition 22. Let
![]() $\rho\;:\;\thinspace \pi_1({\mathcal{O}}_{3,3,3,3}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R) \to PSL(n,\mathbb{Z})$
be the representation defined in (5). Then the restrictions of
$\rho\;:\;\thinspace \pi_1({\mathcal{O}}_{3,3,3,3}) \simeq \pi_1({\mathcal{O}}_L)\ast_{\langle [\gamma] \rangle}\pi_1({\mathcal{O}}_R) \to PSL(n,\mathbb{Z})$
be the representation defined in (5). Then the restrictions of
![]() $\rho$
to
$\rho$
to
![]() $\pi_1({\mathcal{O}}_L)$
and
$\pi_1({\mathcal{O}}_L)$
and
![]() $\pi_1({\mathcal{O}}_R)$
are irreducible.
$\pi_1({\mathcal{O}}_R)$
are irreducible.
Proof. To see that
![]() $\rho|_{\pi_1({\mathcal{O}}_L)}$
is irreducible it suffices to see that the restriction of
$\rho|_{\pi_1({\mathcal{O}}_L)}$
is irreducible it suffices to see that the restriction of
![]() $\omega_n\circ \sigma$
to
$\omega_n\circ \sigma$
to
![]() $\pi_1({\mathcal{O}}_L)$
is irreducible. We have that
$\pi_1({\mathcal{O}}_L)$
is irreducible. We have that
![]() $\sigma(\pi_1({\mathcal{O}}_L))$
is Zariski dense in
$\sigma(\pi_1({\mathcal{O}}_L))$
is Zariski dense in
![]() $PSL(2,\mathbb{R})$
. To see that the representation
$PSL(2,\mathbb{R})$
. To see that the representation
![]() $\omega_n\;:\;\thinspace\sigma(\pi_1({\mathcal{O}}_L)) \to PSL(n,\mathbb{R})$
is irreducible, it is enough to check that the Zariski closure of its image is irreducible. This holds since
$\omega_n\;:\;\thinspace\sigma(\pi_1({\mathcal{O}}_L)) \to PSL(n,\mathbb{R})$
is irreducible, it is enough to check that the Zariski closure of its image is irreducible. This holds since
![]() $\omega_n \;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
is an irreducible representation and a morphism of algebraic groups, so
$\omega_n \;:\;\thinspace PSL(2,\mathbb{R}) \to PSL(n,\mathbb{R})$
is an irreducible representation and a morphism of algebraic groups, so
![]() $\omega_n(PSL(2,\mathbb{R})) = \omega_n(\overline{\sigma(\pi_1({\mathcal{O}}_L)}) \subseteq \overline{\omega_n\circ\sigma(\pi_1({\mathcal{O}}_L))}$
. That
$\omega_n(PSL(2,\mathbb{R})) = \omega_n(\overline{\sigma(\pi_1({\mathcal{O}}_L)}) \subseteq \overline{\omega_n\circ\sigma(\pi_1({\mathcal{O}}_L))}$
. That
![]() $\rho|_{\pi_1({\mathcal{O}}_R)}$
follows from
$\rho|_{\pi_1({\mathcal{O}}_R)}$
follows from
![]() $\sigma(\pi_1({\mathcal{O}}_L))$
being Zariski dense in
$\sigma(\pi_1({\mathcal{O}}_L))$
being Zariski dense in
![]() $PSL(2,\mathbb{R})$
.
$PSL(2,\mathbb{R})$
.
Knowing that
![]() $\rho$
is an integral orbifold Fuchsian representation, the previous proposition shows
$\rho$
is an integral orbifold Fuchsian representation, the previous proposition shows
![]() $\rho$
satisfies the assumptions of Theorem 19. Thus we obtain the following application of Corollary 20.
$\rho$
satisfies the assumptions of Theorem 19. Thus we obtain the following application of Corollary 20.
Theorem 23. For every surface S finitely covering the orbifold
![]() $O_{3,3,3,3}$
and every odd
$O_{3,3,3,3}$
and every odd
![]() $n>1$
there exists a path of Hitchin representations
$n>1$
there exists a path of Hitchin representations
![]() $\rho_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
, so that:
$\rho_t \;:\;\thinspace \pi_1(S) \to SL(n,\mathbb{R})$
, so that:
-
(i)
 $\rho_0(\pi_1(S)) \subset SL(n,\mathbb{Z})$
;
$\rho_0(\pi_1(S)) \subset SL(n,\mathbb{Z})$
; -
(ii)
 $\rho_t$
is Zariski dense for every
$\rho_t$
is Zariski dense for every
 $t>0$
; and
$t>0$
; and -
(iii)
 $\rho_t(\pi_1(S)) \subset SL(n,\mathbb{Q})$
for every
$\rho_t(\pi_1(S)) \subset SL(n,\mathbb{Q})$
for every
 $t\in \mathbb{Q}$
.
$t\in \mathbb{Q}$
.
Acknowledgments
This research was completed at UCSB’s Mathematics Department as part of my doctoral dissertation. I am grateful for the help towards its completion.