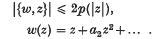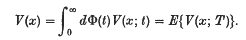Research Article
Representations of holomorphs of group extensions with Abelian kernels
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-368
-
- Article
- Export citation
Dualizing complexes for commutative Noetherian rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-386
-
- Article
- Export citation
A proof of Sperner's lemma via Hall's theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 387
-
- Article
- Export citation
Convex polytopes with convex nets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-403
-
- Article
- Export citation
Spectral asymmetry and Riemannian geometry. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 405-432
-
- Article
- Export citation
Measures of the non-convexity of sets and the Shapley–Folkman–Starr theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-436
-
- Article
- Export citation
Congruence properties of the binary partition function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 437-442
-
- Article
- Export citation
On a conjecture of Littlewood
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-445
-
- Article
- Export citation
A proof of Hartman's theorem on compact Hankel operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-450
-
- Article
- Export citation
On Toeplitz sections in sequence spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-460
-
- Article
- Export citation
Positive-moment problems in abstract measure spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 461-469
-
- Article
- Export citation
Lp(G)-isotone measures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 471-481
-
- Article
- Export citation
On the comparison of measure functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-491
-
- Article
- Export citation
A general Bieberbach inequality
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 493-495
-
- Article
- Export citation
Gap Tauberian theorem for generalized Abel summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-500
-
- Article
- Export citation
The Schwarzian derivative and estimates of functions analytic in the unit disc
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 501-511
-
- Article
- Export citation
A characterization of the Poisson process using forward recurrence times
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 513-516
-
- Article
- Export citation
The reflection of short gravity waves on a non-uniform current
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 517-525
-
- Article
- Export citation
Meeting Report
Proceedings of the meetings held during the session 1974–75
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-532
-
- Article
- Export citation
Front matter
PSP volume 78 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation

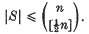
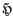 . In particular they give a proof, much simpler and under less restrictive conditions, of results due to Shapley, Folkman and Starr which are of importance in Mathematical Economics ((1),(2)).
. In particular they give a proof, much simpler and under less restrictive conditions, of results due to Shapley, Folkman and Starr which are of importance in Mathematical Economics ((1),(2)).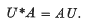
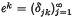 form a Toeplitz basis. In section 3, we present characterizations of Toeplitz sectional boundedness (
form a Toeplitz basis. In section 3, we present characterizations of Toeplitz sectional boundedness (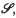 µ). We suppose throughout that
µ). We suppose throughout that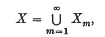
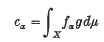
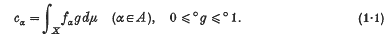
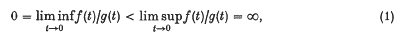
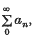 write
write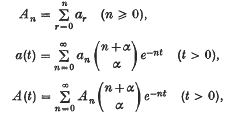
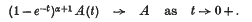
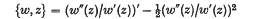
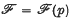 denote the class of functions
denote the class of functions