Research Article
Locally finite minimal non-FC-groups
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 417-420
-
- Article
- Export citation
Endomorphisms of free groups and their fixed points
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 421-422
-
- Article
- Export citation
Carlson varieties and Chouinard's theorem
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 423-439
-
- Article
- Export citation
Hilbert functions and the extension functor
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 441-446
-
- Article
- Export citation
Pure ring extensions and self FP-injective rings
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 447-458
-
- Article
- Export citation
An elementary proof and an extension of Thas' theorem on k-arcs
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 459-462
-
- Article
- Export citation
A Godement theorem for locales
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 463-471
-
- Article
- Export citation
A model in which countable Fréchet α1-spaces are first countable
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 473-480
-
- Article
- Export citation
A Tauberian theorem concerning Dirichlet series
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 481-484
-
- Article
- Export citation
Properties of Littlewood-Paley sets
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 485-494
-
- Article
- Export citation
Characterization of inverse-closed Beurling classes
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 495-501
-
- Article
- Export citation
On the p-approximate property for hypersurfaces of ℝn
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 503-511
-
- Article
- Export citation
Continuity of the generalized kernel and range of semi-Fredholm operators
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 513-522
-
- Article
- Export citation
Small Riesz spaces
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 523-536
-
- Article
- Export citation
Kasparov's technical lemma for b*-algebras
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 537-545
-
- Article
- Export citation
Metric Diophantine approximation and Hausdorff dimension on manifolds
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 547-558
-
- Article
- Export citation
Zeros of expansions in orthogonal polynomials
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 559-573
-
- Article
- Export citation
A large deviation local limit theorem
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 575-577
-
- Article
- Export citation
Linear functionals and Markov chains associated with Dirichlet processes
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 579-585
-
- Article
- Export citation
Some eigenvalue identities for Brownian motion
-
- Published online by Cambridge University Press:
- 04 October 2011, pp. 587-596
-
- Article
- Export citation

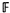
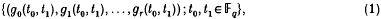
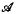 is a countable family of sequences converging to it, there is a sequence
is a countable family of sequences converging to it, there is a sequence 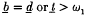 and has asked if it is consistent that no such space exists. It is not difficult to see that if there is an α
and has asked if it is consistent that no such space exists. It is not difficult to see that if there is an α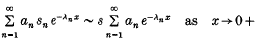
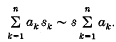
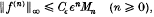
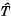 ε
ε