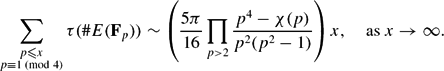Research Article
Subgroup properties of Demushkin groups†
-
- Published online by Cambridge University Press:
- 05 October 2015, pp. 1-9
-
- Article
- Export citation
Non-commutative Iwasawa theory for elliptic curves with multiplicative reduction
-
- Published online by Cambridge University Press:
- 15 October 2015, pp. 11-38
-
- Article
- Export citation
Real zeros of Hurwitz–Lerch zeta and Hurwitz–Lerch type of Euler–Zagier double zeta functions
-
- Published online by Cambridge University Press:
- 12 October 2015, pp. 39-50
-
- Article
- Export citation
Generalised Cantor sets and the dimension of products
-
- Published online by Cambridge University Press:
- 30 October 2015, pp. 51-75
-
- Article
- Export citation
Positive definite *-spherical functions, property (T) and C*-completions of Gelfand pairs
-
- Published online by Cambridge University Press:
- 26 October 2015, pp. 77-93
-
- Article
- Export citation
Fast escaping points of entire functions: a new regularity condition
-
- Published online by Cambridge University Press:
- 29 October 2015, pp. 95-106
-
- Article
- Export citation
The Hasse principle for lines on diagonal surfaces
-
- Published online by Cambridge University Press:
- 30 October 2015, pp. 107-119
-
- Article
- Export citation
Homology stability for symmetric diffeomorphism and mapping class groups
-
- Published online by Cambridge University Press:
- 02 December 2015, pp. 121-139
-
- Article
- Export citation
Motivic invariants of real polynomial functions and their Newton polyhedrons
-
- Published online by Cambridge University Press:
- 26 November 2015, pp. 141-166
-
- Article
- Export citation
A Titchmarsh divisor problem for elliptic curves
-
- Published online by Cambridge University Press:
- 10 November 2015, pp. 167-189
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 160 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 December 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 160 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 December 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation