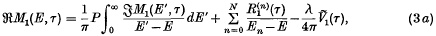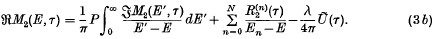Research Article
A second note on the simple group of order 6048
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-9
-
- Article
- Export citation
The Wiener–Pitt phenomenon on semi-groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-24
-
- Article
- Export citation
Concerning automorphisms in finitely generated Abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-31
-
- Article
- Export citation
On a problem of Erdős concerning decompositions of the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-36
-
- Article
- Export citation
On the Steinhaus billiard table problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-41
-
- Article
- Export citation
On a potential-theoretic example of Kiang
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-46
-
- Article
- Export citation
On the Nörlund summability of Fourier series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 47-53
-
- Article
- Export citation
On the solutions of the Low equation*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-61
-
- Article
- Export citation
Integral transforms based upon fractional integration
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 63-71
-
- Article
- Export citation
Asymptotic expansions of generalized Bernoulli polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-80
-
- Article
- Export citation
Approximate integration of rapidly oscillating functions and of periodic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-88
-
- Article
- Export citation
On Coulomb wave functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-94
-
- Article
- Export citation
Uniform approximate solutions of certain nth-order differential equations. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-110
-
- Article
- Export citation
Further results for the solutions of a third-order differential equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-116
-
- Article
- Export citation
The solution of an infinite set of differential-difference equations occurring in polymerization and queueing problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-124
-
- Article
- Export citation
The system of inequalities ars > Xr—Xs*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 125-133
-
- Article
- Export citation
On inequalities of the Tchebychev type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-146
-
- Article
- Export citation
Hamiltonian approach to the method of summation over Feynman histories
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-155
-
- Article
- Export citation
An inequality in Feynman integrands
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-160
-
- Article
- Export citation
Dispersion relations for a two-channel scattering process: residues of the scattering amplitudes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-166
-
- Article
- Export citation

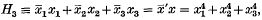
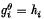 (
( that if
that if 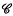 be a plane closed convex curve, and regard
be a plane closed convex curve, and regard 
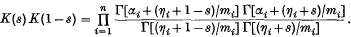

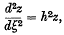


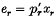 so that
so that 
 (typically finite-dimensional Euclidean space). Then the problem is to set bounds for E
(typically finite-dimensional Euclidean space). Then the problem is to set bounds for E