Research Article
Remarks on the Dirac δ-operator
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-494
-
- Article
- Export citation
On non-linear differential equations of the second order: III. The equation ẍ − k(1 − x2)ẋ + x = p.kλ cos (λt + α), k small and λ near 1.
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 495-501
-
- Article
- Export citation
An inequality in the theory of arithmetic on algebraic varieties
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 502-509
-
- Article
- Export citation
A further inequality in the theory of arithmetic on algebraic varieties
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 510-518
-
- Article
- Export citation
The Kummer quartic and the tetrahedroids based on the Maschke forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 519-535
-
- Article
- Export citation
Note on some properties of maximum likelihood estimates
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 536-544
-
- Article
- Export citation
The exact transition probabilities of quantum-mechanical oscillators calculated by the phase-space method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-553
-
- Article
- Export citation
The tabulation of Bessel functions for large argument
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 554-557
-
- Article
- Export citation
The formation and growth of shock waves in the one-dimensional motion of a gas
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 558-586
-
- Article
- Export citation
Elastic stability of infinite strips
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 587-594
-
- Article
- Export citation
Rectilinear flow of non-Bingham plastic solids and non-Newtonian viscous liquids. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 595-611
-
- Article
- Export citation
Notes on the forces acting on a two-dimensional aerofoil in shear flow in the presence of a plane boundary
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 612-620
-
- Article
- Export citation
Axial symmetric stress distributions in aeolotropic hexagonal crystals. The problem of the plane and related problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 621-630
-
- Article
- Export citation
An approximate relation between the energy levels of a particle in a field of given potential energy, calculated on the relativistic and non-relativistic theories
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 631-637
-
- Article
- Export citation
A modification of the molecular orbital method: the LCMO method
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 638-647
-
- Article
- Export citation
The theory of counting experiments using pulsed sources: chance coincidences and counting-rate losses
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 648-659
-
- Article
- Export citation
The forces between floating bubbles and a quantitative study of the Bragg ‘Bubble Model’ of a crystal
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 660-673
-
- Article
- Export citation
Research Notes
A short proof of a theorem on reflexive spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 674
-
- Article
- Export citation
The values taken by a rational function on an algebraic variety
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 675-677
-
- Article
- Export citation
Stark effect for a hydrogen atom in its ground state
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 678-679
-
- Article
- Export citation

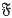
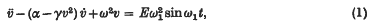

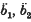 can be neglected, and ḃ
can be neglected, and ḃ