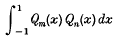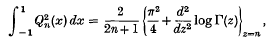Research Notes
On p-quotients and star diagrams of the symmetric group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 157-160
-
- Article
- Export citation
Extremal lattices of convex bodies
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-162
-
- Article
- Export citation
Some properties of Legendre functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 162-164
-
- Article
- Export citation
A short proof of the Minkowski-Hlawka theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-166
-
- Article
- Export citation
Stability of plane parallel flows of electrically conducting fluids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-168
-
- Article
- Export citation
A note on Stokes's stream function for motion with a spherical boundary
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 169-174
-
- Article
- Export citation
Front matter
PSP volume 49 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 49 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation