Research Article
Conformal frames and field equations in a conformal theory of ǵravitation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-414
-
- Article
- Export citation
On the analyticity of static vacuum solutions of Einstein's equations†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 415-421
-
- Article
- Export citation
On the short-wave asymptotic motion due to a cylinder heavinǵ on water of finite depth. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 423-442
-
- Article
- Export citation
On the short-wave asymptotic motion due to a cylinder heaving on water of finite depth. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-468
-
- Article
- Export citation
Boundary layers in micropolar liquids
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-476
-
- Article
- Export citation
A ‘stick-slip’ problem related to the motion of a free jet at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-489
-
- Article
- Export citation
Exact solutions for vertically polarized electromaǵnetic waves in a horizontally stratified maǵneto-plasma
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-501
-
- Article
- Export citation
On monotonicity of the relaxation functions of viscoelastic materials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 503-508
-
- Article
- Export citation
Determination of phase velocities of a circular helix using the method of internal constraints
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 509-521
-
- Article
- Export citation
Linked-cluster expansions for the correlation functions of lattice systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-534
-
- Article
- Export citation
Fornt matter
PSP volume 67 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
- Export citation
Back matter
PSP volume 67 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

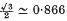 for the axisymmetric case, and
for the axisymmetric case, and 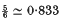 for the two-dimensional case (see Harmon (8)). By treating the dynamics of the jet as those of a boundary layer growing on the free surface, Goren and Wronski (6) and Tillett (18) are able to examine the flow in greater detail.
for the two-dimensional case (see Harmon (8)). By treating the dynamics of the jet as those of a boundary layer growing on the free surface, Goren and Wronski (6) and Tillett (18) are able to examine the flow in greater detail.