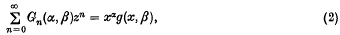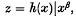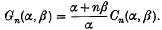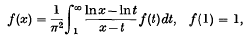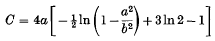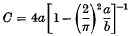Research Article
Some arithmetical properties of m-ary partitions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-453
-
- Article
- Export citation
On the remainder in the two-dimensional central limit theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 455-458
-
- Article
- Export citation
A generalized Vandermonde-type convolution and associated inverse series relations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-474
-
- Article
- Export citation
On the geometric structure of classical field theory in Lagrangian formulation†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-484
-
- Article
- Export citation
The theory of trailing Taylor columns
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-491
-
- Article
- Export citation
The effects of strong suction on laminar boundary layers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 493-508
-
- Article
- Export citation
A small unsteady perturbation on the steady hydromagnetic boundary-layer flow past a semi-infinite plate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 509-528
-
- Article
- Export citation
A Wiener-Hopf solution to the triple integral equations for the electrified disc in a coplanar gap
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 529-545
-
- Article
- Export citation
The Rikitake two-disc dynamo system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 547-569
-
- Article
- Export citation
Internal labelling: the classical groups†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 571-578
-
- Article
- Export citation
Front matter
PSP volume 68 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 68 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation


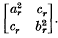
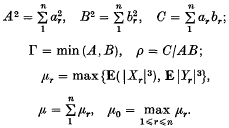
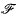 (
(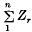 and let
and let 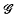 (
(